Bài giảng Hình học Lớp 8 - Chương 3, Bài 5: Trường hợp đồng dạng thứ nhất

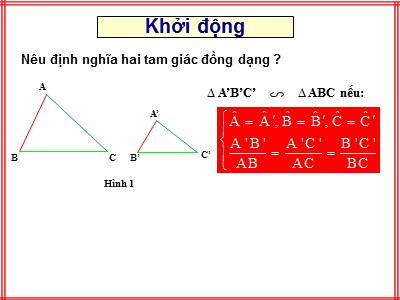
Khởi độngNêu định nghĩa hai tam giác đồng dạng ? A B C A’ B’ C’ Hình 1 ∆ A’B’C’ ∆ ABC nếu:Nếu tam giác A’B’C’ và tam giác ABC có thì ∆A’B’C’ và ∆ABC có đồng dạng không??1: Hai tam giác ABC và A’B’C’ có các kích th­ước nh­ư hình 32 ( có cùng đơn vị đo là cm).+ Trên các cạnh AB và AC của tam giác ABC lần l­ượt lấy hai điểm M, N sao cho AM = A’B’ = 2 cm; AN = A’C’ = 3 cm.+ Tính độ dài đoạn thẳng MN?+ Có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN và A’B’C’?Hình 32ABCA’B’C’4862342BCAMNDo: AB = 4cm; AC = 6cm; AM = 2cm; AN = 3cmTừPhương pháp chứng minh:A'C’B'BCAMNBước 1: Dựng AMN đồng dạng với tam giác ABC và AM = A’B’Bước 2: Chứng minh: AMN = A’B’C’ Từ đó suy ra A’B’C’ đồng dạng với ABCΔA’B’C’ ΔABC GTKL=> ∆AMN ∆ABC (định lý) , mà AM = A’B’Lại có: Từ (1) và (2) suy ra: Nên: ∆A’B’C’ ∆ABCChứng minh N(1) (2) Trên AB lấy M sao cho AM = A’B’Do MN // BC (N thuộc AC) Hay: AN = A’C’ ; MN = B’C’ mà: ∆AMN ∆ABC (cmt )MABC6810A’B’C’3 45Bài tập 1: Cho hình vẽ	 	 A’B’C’ ABC không? Vì Sao?Bài tập 2: Hai tam giác sau có đồng dạng với nhau không?Ta có: Nên hai tam giác đã cho không đồng dạng với nhau.Hãy nhận xét lời giải trên? Đáp án Bài tập 2:Ta có: 	 Suy ra	 A’B’C’ BCA (c.c.c)Chú ýNếu ΔABC đồng dạng với ΔA’B’C’; ΔABC không đồng dạng với ΔXYZ thì ΔA’B’C’cũng không đồng dạng với ΔXYZ .Khi lập tỉ số giữa các cạnh của hai tam giác ta phải lập tỉ số giữa hai cạnh lớn nhất của hai tam giác, tỉ số giữa hai cạnh nhỏ nhất của hai tam giác, tỉ số giữa hai cạnh còn lại rồi so sánh ba tỉ số đó với nhau.?2. Tìm trong hình vẽ 34 các cặp tam giác đồng dạng? 846432546BCAEFDIKHXét ABC và DFE có: => ABC DFE (c.c.c) b) Tính tỉ số chu vi của hai tam giác ABC và A’B’C’ :a) ABC và A’B’C’ có :Bài 29: Cho hai tam giác ABC và A’B’C’ có kích thước như hình 35. ABC và A’B’C’ có đồng dạng với nhau không ? Vì sao?Tính tỉ số chu vi của hai tam giác trên .A'C'B'BCAHình 35 Theo câu a, ta có:6912468 ABC A’B’C’ (c-c-c)H­ướng dẫn tự học ở nhàLàm bài tập 30, 31 trang 75 SGK, SBT.Đọc và tìm hiểu bài: “Tr­ường hợp đồng dạng thứ hai ”.- Chuẩn bị thư­ớc thẳng, compa, êke, th­ước đo góc.Bài 30: Tam giác ABC có: AB = 3cm, AC = 5cm, BC = 7cm. Tam giác A’B’C’ đồng dạng với tam giác ABC và có chu vi bằng 55cm.? Hãy tính độ dài các cạnh của tam giác A’B’C’ (làm tròn đến chữ số thập phân thứ hai)H­DTa có ∆A’B’C’ ∆ABC (gt)Áp dụng tính chất dãy tỉ số bằng nhau ta có: Từ đó tính được: A’B’ ; B’C’ ; A’C’ Gọi hai cạnh tương ứng là A’B’ và AB, có AB - A’B’ = 12,5 (cm) Từ đó tính được: A’B’ ; AB Ta có ∆A’B’C’ ∆ABC (gt)Bài 31: Cho hai tam giác đồng dạng có tỉ số chu vi là và hiệu độ dài hai cạnh t­ương ứng của chúng là 12,5cm.? Tính hai cạnh đó. H­D