Bài giảng môn Hình học Lớp 8 - Tiết 42, Bài 4: Khái niệm hai tam giác đồng dạng
Tính chất :
- Tính chất 1 : Mỗi tam giác đồng dạng với chính nó.
- Tính chất 2: Nếu ?A’B’C’ ?ABC thì ?ABC ?A’B’C’.
Tính chất 3: Nếu ?A’B’C’ ?A”B”C” và ?A”B”C” ?ABC thì
?A’B’C’ ?ABC.
Định lý :
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
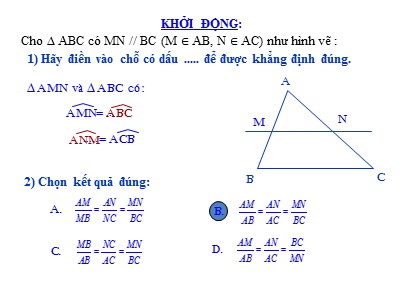
Chứng minh: Xét tam giác ABC có MN // BC có:
AMN = ABC ; ANM = ACB (Các cặp góc đồng vị)
BAC là góc chung.
Mặt khác : MN // BC theo hệ quả của định lý Ta lét ta có :
Suy ra AMN ABC.
Bạn đang xem tài liệu "Bài giảng môn Hình học Lớp 8 - Tiết 42, Bài 4: Khái niệm hai tam giác đồng dạng", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
KHỞI ĐỘNG: Cho ∆ ABC có MN // BC (M ∈ AB, N ∈ AC) như hình vẽ :ABCMN1) Hãy điền vào chỗ có dấu ..... để được khẳng định đúng.∆ AMN vµ ∆ ABC cã:= ACB 2) Chọn kết quả đúng:A.B.C.D.AMN=........ABCANMa. Định nghĩa: A’ = A;B’ = B;C’ = C===>Giải:Ta có A’ = A;B’ = B;C’ = CABCA’B’C’= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCSỞ ?1 có tỉ số đồng dạng k =?k = 1/2?1A’C’B’232,5ABC456Cho hai tam giác ABC và A’B’C’Hãy viết các cặp góc bằng nhau.-Tính các tỉ số ,so sánh Cần viết đúng các đỉnh tương ứng Δ A’B’C’ đồng dạng với Δ ABC nếuTiÕt 42. Kh¸i niÖm hai tam gi¸c ®ång d¹ng1. Tam gi¸c ®ång d¹ng Ta nói ΔA’B’C’ đồng dạng với ΔABC1. Tam gi¸c ®ång d¹ngDEF345ABCA’B’C’465232,5V× sao ∆ DEF kh«ng ®ång d¹ng víi ∆ ABC ?TiÕt 42. Kh¸i niÖm hai tam gi¸c ®ång d¹nga. Định nghĩa:A’ = A;B’ = B;C’ = C= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCS Δ A’B’C’ đồng dạng với Δ ABC nếuTiÕt 42. Kh¸i niÖm hai tam gi¸c ®ång d¹ng1. Tam gi¸c ®ång d¹ngΔA’B’C’ = ΔABCA’ = A ; B’ = B ; C’ = Cvà ΔA’B’C’ ΔABCSA’B’=AB, A’C’=AC, B’C’=BC vàA’ = A ; B’ = B ; C’ = CAA’B’BC’CTa có bảng so sánh:b. Tính chất:??=1a. Định nghĩa:A’ = A;B’ = B;C’ = C= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCS Δ A’B’C’ đồng dạng với Δ ABC nếu1. Tam giác đồng dạngb. Tính chất:1) Nếu A’B’C’ = ABC thì A’B’C’ có đồng dạng với ABC không ? Tỉ số đồng dạng là bao nhiêu?2) Nếu A’B’C’ ABC theo tØ sè k th× ABC A’B’C’ theo tØ sè nµo ?ssLêi gi¶i. 1) A’B’C’ = ABC A’B’C’ ABC ( tỉ số đồng dạng k= 1) s A’B’C’ ABC theo tỉ số k s?2= ? sVậy AB C A’B’C’ theo tỉ số a. Định nghĩa:A’ = A;B’ = B;C’ = C= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCS Δ A’B’C’ đồng dạng với Δ ABC nếuTiÕt 42. Kh¸i niÖm hai tam gi¸c ®ång d¹ng1. Tam gi¸c ®ång d¹ngb. Tính chất: (sgk/70)TÝnh chÊt :- TÝnh chÊt 1 : Mçi tam gi¸c ®ång d¹ng víi chÝnh nã.- TÝnh chÊt 2: NÕu A’B’C’ ABC th× ABC A’B’C’. TÝnh chÊt 3: NÕu A’B’C’ A”B”C” vµ A”B”C” ABC th× A’B’C’ ABC.sssssKHỞI ĐỘNG Cho ∆ ABC có MN // BC (M ∈ AB, N ∈ AC) như hình vẽ:ABCMN1) Hãy điền vào chỗ có dấu ..... để được khẳng định đúng:∆ AMN và ∆ ABC có:= ACB 2) Chọn kết quả đúng:A.B.C.D.AMN=........ABCANMEm cã nhËn xÐt g× vÒ ∆ AMN vµ ∆ ABC ? A là góc chung AMN ABC.s(MN // BC) a. Định nghĩa:A’ = A;B’ = B;C’ = C= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCS Δ A’B’C’ đồng dạng với Δ ABC nếu1. Tam giác đồng dạngb. Tính chất: (sgk/70)2. §Þnh lý : (SGK/ 71)Định lý : Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.ABCMNaGT ABC , MN // BC ( M AB, N AC )KL AMN ABCss Mặt khác : MN // BC theo hệ quả của định lý Ta lét ta có : Suy ra AMN ABC.Chứng minh: Xét tam giác ABC có MN // BC có:AMN = ABC ; ANM = ACB (Các cặp góc đồng vị) BAC là góc chung.a. Định nghĩa:A’ = A;B’ = B;C’ = C= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCS Δ A’B’C’ đồng dạng với Δ ABC nếu1. Tam gi¸c ®ång d¹ngb. Tính chất: (sgk/70)2. §Þnh lý : (SGK/ 71)ABCMNaGT ABC , MN // BC ( M AB, N AC )KL AMN ABCsABCMNaABCMNaMNMNChú ý: Định lý cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại. + Chó ý: (sgk/71) 15436SAO MAY MẮN2ABCMNC©u 1. Chän ®¸p ¸n ®óng:Cho ∆ ABC cã MN // AC ta cã:A. ∆ BMN ∆ BCAB. ∆ ABC ∆ MBNC. ∆ BMN ∆ ABCD. ∆ ABC ∆ MNBssss 0 : 00 0 : 01 0 : 02 0 : 03 0 : 04 0 : 05 0 : 06 0 : 07 0 : 08 0 : 09 0 : 10 0 : 11 0 : 12 0 : 13 0 : 14 0 : 15 0 : 16 0 : 17 0 : 18 0 : 19 0 : 20 0 : 21 0 : 22 0 : 20 0 : 23 0 : 24 0 : 25 0 : 26 0 : 27 0 : 28 0 : 29 0 : 30C©u 2. MÖnh ®Ò nµo ®óng, mÖnh ®Ò nµo sai ?Hai tam gi¸c b»ng nhau th× ®ång d¹ng víi nhau.b) Hai tam gi¸c ®ång d¹ng víi nhau th× b»ng nhau.S§ 0 : 00 0 : 01 0 : 02 0 : 03 0 : 04 0 : 05 0 : 06 0 : 07 0 : 08 0 : 09 0 : 10 0 : 11 0 : 12 0 : 13 0 : 14 0 : 15 0 : 16 0 : 17 0 : 18 0 : 19 0 : 20 0 : 21 0 : 22 0 : 20 0 : 23 0 : 24 0 : 25 0 : 26 0 : 27 0 : 28 0 : 29 0 : 30SAO MAY MẮNSAO KHÔNG MAY MẮNA. 2 B. 1C. D. C¶ 3 c©u trªn ®Òu sai.C©u 3. Chän ®¸p ¸n ®óng.NÕu ∆ ABC ∆ A’B’C’ theo tØ sè th× ∆ A’B’C’ ∆ ABC theo tØ sè:ss 0 : 00 0 : 01 0 : 02 0 : 03 0 : 04 0 : 05 0 : 06 0 : 07 0 : 08 0 : 09 0 : 10 0 : 11 0 : 12 0 : 13 0 : 14 0 : 15 0 : 16 0 : 17 0 : 18 0 : 19 0 : 20 0 : 21 0 : 22 0 : 20 0 : 23 0 : 24 0 : 25 0 : 26 0 : 27 0 : 28 0 : 29 0 : 30C©u 4. Trong c¸c kh¼ng ®Þnh sau, kh¼ng ®Þnh nµo ®óng,Kh¼ng ®Þnh nµo sai ? ∆ ABC vµ ∆ DEF cã A = 80 , B = 70 NÕu ∆ ABC ∆ DEF th×:A) D = 80B) E = 80C) F = 70D) C = 30S§sooooooS§ 0 : 00 0 : 01 0 : 02 0 : 03 0 : 04 0 : 05 0 : 06 0 : 07 0 : 08 0 : 09 0 : 10 0 : 11 0 : 12 0 : 13 0 : 14 0 : 15 0 : 16 0 : 17 0 : 18 0 : 19 0 : 20 0 : 21 0 : 22 0 : 20 0 : 23 0 : 24 0 : 25 0 : 26 0 : 27 0 : 28 0 : 29 0 : 30a. Định nghĩa:A’ = A;B’ = B;C’ = C= kk gọi là tỉ số đồng dạngKí hiệu: ΔA’B’C’ ΔABCS Δ A’B’C’ đồng dạng với Δ ABC nếu1. Tam gi¸c ®ång d¹ngb. Tính chất: (sgk/70)2. §Þnh lý : (SGK/ 71)ABCMNaGT ABC , MN // BC ( M AB, N AC )KL AMN ABCs + Chó ý: (sgk/71) HƯỚNG DẪN VỀ NHAØ-Nắm vững định nghĩa,định lí,tính chất hai tam giác đồng dạng-BTVN:24,25,27 tr 72 SGK 25,26 tr 71 SBT -Tiết sau luyện tập.Hướng dẫn BT 24 SGK A’B’C’ A”B”C” S A’’B’’C’’ ABCS A’ B’C’ ABCSk1.k2
Tài liệu đính kèm:
 bai_giang_mon_hinh_hoc_lop_8_tiet_42_bai_4_khai_niem_hai_tam.pptx
bai_giang_mon_hinh_hoc_lop_8_tiet_42_bai_4_khai_niem_hai_tam.pptx



