Bài giảng Hình học Lớp 8 - Tiết 37, Bài 1: Định lý Talet trong tam giác
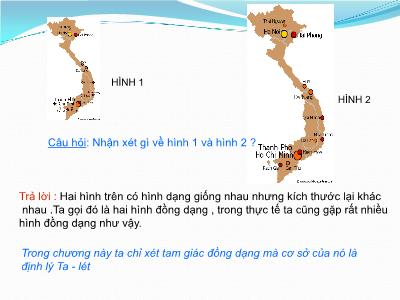
Trả lời : Hai hình trên có hình dạng giống nhau nhưng kích thước lại khác
nhau .Ta gọi đó là hai hình đồng dạng , trong thực tế ta cũng gặp rất nhiều
hình đồng dạng như vậy.
Trong chương này ta chỉ xét tam giác đồng dạng mà cơ sở của nó là định lý Ta - lét
* Nội dung chính của chương gồm:
- Định lý Ta – lét ( thuận, đảo và hệ quả).
- Tính chất đường phân giác của tam giác.
- Tam giác đồng dạng và các ứng dụng của nó
* Định nghĩa : Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Bạn đang xem 20 trang mẫu của tài liệu "Bài giảng Hình học Lớp 8 - Tiết 37, Bài 1: Định lý Talet trong tam giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
HÌNH 1HÌNH 2Câu hỏi: Nhận xét gì về hình 1 và hình 2 ?Trả lời : Hai hình trên có hình dạng giống nhau nhưng kích thước lại khác nhau .Ta gọi đó là hai hình đồng dạng , trong thực tế ta cũng gặp rất nhiều hình đồng dạng như vậy.Trong chương này ta chỉ xét tam giác đồng dạng mà cơ sở của nó là định lý Ta - létChương III – TAM GIÁC ĐỒNG DẠNG* Nội dung chính của chương gồm:- Định lý Ta – lét ( thuận, đảo và hệ quả).- Tính chất đường phân giác của tam giác.- Tam giác đồng dạng và các ứng dụng của nó §1. ĐỊNH LÝ TA - LÉT TRONG TAM GIÁC1.Tỉ số của hai đoạn thẳng:Tỉ số hai đoạn thẳng là gì ?TIẾT: 37Bài tập: Cho hai số 3 và 5 . Hãy tính tỉ số của nó :Giải: Tỉ số của hai số 3 và 5 là : Cho AB = 3 cm; CD = 5 cm. ?1ABCD Cho EF = 4 dm; MN = 7 dm.TIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:TIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:Vậy tỉ số hai đoạn thẳng là gì ? * Định nghĩa : Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.Tỉ số của hai đoạn thẳng AB và CD kí hiệu là:Nếu AB = 300cm, CD = 400cm thì:Nếu AB = 3m, CD = 4m thì Nếu EF = 48cm, GH = 16dm thì ta cũng có :Ví dụ:* Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo.?2Cho bốn đoạn thẳng AB, CD, A’B’, C’D’ như hình sau:ABCDA’B’C’D’ So sánh các tỉ số =vàTIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:Định nghĩa: (SGK)2.Đoạn thẳng tỉ lệ :Ta nói hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng A’B’ và C’D’TIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:Định nghĩa: (SGK)2.Đoạn thẳng tỉ lệ :Vậy AB và CD gọi là tỉ lệ với A’B’ và C’D’ khi nào ?Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳngA’B’ và C’D’ nếu có tỉ lệ thức: Định nghĩa: hayabcdABCDEFGHHãy so sánh độ dài các đoạn EF, FG, GHEF = FG = GHCác đường thẳng song song cách đềuVậy : Các đường thẳng song song cách đều cắt 1 đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.ABCB’C’a?3/SGKHãy so sánh các tỉ số:===TIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:Định nghĩa: (SGK)2.Đoạn thẳng tỉ lệ :Định nghĩa: (SGK) 3.Định lý Ta-lét trong tam giác Hoạt động nhóm: ? Nhóm 1 thực hiện câu a ; nhóm 2 thực hiện câu b; nhóm 3, 4 thực hiện câu c ( thời gian là 2 phút)Hết giờ1236912369Qua ? 3 ta rút ra được kết luận gì ? Khi một đường thẳng song song với một cạnh tam và cắt hai cạnh còn lại của tam giác. TIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:Định nghĩa: (SGK)2.Đoạn thẳng tỉ lệ :Định nghĩa: (SGK) 3.Định lý Ta-lét trong tam giácNếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.Định lý Ta-létAB’C’BC ABC, (B’ AB,C’ AC) B’C’ // BCGTKL12345TRÒ CHƠI: NGÔI SAO MAI MẮN132451Câu : aHãy chọn câu trả lời đúng trong hai câu trả lời sau:Ví dụ : Tính độ dài x trong hình sau:DMNEFBiết rằng: MN // EFGiảiVì MN // EF, theo định lí Ta-lét ta có:6,5x421HEÁT GIÔØ2345678 9102Bài giải sau ®óng hay sai?SaiADEBC510xTính độ dài x trong hình sau:GiảiVì DE // BC (do a//BC), theo định lí Ta-lét ta có:Biết rằng: a // BC12345678910HEÁT GIÔØ3C©u: bHãy chọn câu trả lời đúng trong hai câu trả lời sau:Tính độ dài y trong hình sau:ED53,5BAC4yGiảiVì DE // AB (cùng vuông góc với AC),theo định lí Ta-lét ta có: Mà CA = CE + EA = 4 +2,8 = 6,8 y = 6,8a) y = 2,8b) y = 6,8C2 :Vì DE // AB (cùng vuông góc với AC), theo định lí Ta-lét ta có:C1 :4Đ©y lµ ng«i sao may m¾nB¹n ®ưîc quyÒn chän thªm mét ng«i sao5Đ©y lµ ng«i sao kh«ng may m¾nABDCEỨng dụng vào thực tế Chiều cao của người bằng chiều cao của cọc1,5m1,5m8,5m2,1m14m9,8m10m Vì DE // AC (cùng vuông góc với BC), theo định lí Ta-lét ta có:Áp dụng định lý Py-ta-go trong tam giác ABC vuông tại B ta có : AC = 9,8mChiều cao của cây là 9,8mTIẾT:37 §1 .Định lý Ta – lét trong tam giác1.Tỉ số của hai đoạn thẳng:Định nghĩa: 2.Đoạn thẳng tỉ lệ :Định nghĩa: 3.Định lý Ta-lét trong tam giácNếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.Định lý Ta-létTỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’và C’D’ nếu có tỉ lệ thức: hayHưíng dÉn tự học ở nhµ Xem trước nội dung bài : “Định lý đảo và hệ quả của định lý Ta – lét”1. Đối với tiết học này: - Học thuộc các định nghĩa và định lý Ta – lét - Làm lại các ví dụ và các ? đã giải - Làm bài tập 1 , 2, 3 và 5 SGK / 582. Đối với tiết học sau: Đôi nét về nhà toán học Ta-lét (Thalès)Thalès được xem là một trong những nhà hình học đầu tiên của Hi Lạp.Ông sinh vào khoảng năm 624 và mất vào khoảng năm 547 trước Công nguyên, tại thành phố Mi-lê giàu có nhất thời cổ Hi Lạp, nằm trên bờ biển Địa Trung Hải ấp áp và thơ mộng.
Tài liệu đính kèm:
 bai_giang_hinh_hoc_lop_8_tiet_37_bai_1_dinh_ly_talet_trong_t.ppt
bai_giang_hinh_hoc_lop_8_tiet_37_bai_1_dinh_ly_talet_trong_t.ppt



