Đề và đáp án thi chọn học sinh giỏi huyện Toán Lớp 6 - Năm học 2018-2019 - Phòng GD & ĐT Diễn Châ
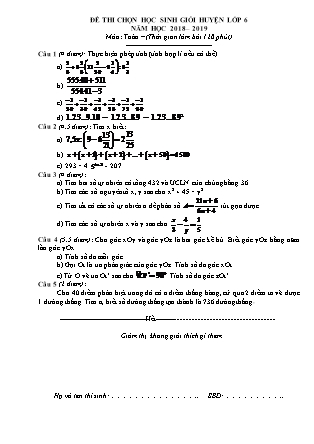
Câu 3 (4 điểm):
a) Tìm hai số tự nhiên có tổng 432 và ƯCLN của chúng bằng 36.
b) Tìm các số nguyên tố x, y sao cho x2 + 45 = y2
c) Tìm tất cả các số tự nhiên n để phân số rút gọn được.
d) Tìm các số tự nhiên x và y sao cho
Câu 4 (5.5 điểm): Cho góc xOy và góc yOz là hai góc kề bù. Biết góc yOz bằng năm lần góc yOx.
a) Tính số đo mỗi góc.
b) Gọi Ot là tia phân giác của góc yOz. Tính số đo góc xOt.
c) Từ O vẽ tia Ot’ sao cho . Tính số đo góc zOt’.
Câu 5 (2 điểm):
Cho 40 điểm phân biệt trong đó có a điểm thẳng hàng, cứ qua 2 điểm ta vẽ được 1 đường thẳng. Tìm a, biết số đường thẳng tạo thành là 736 đường thẳng.
Bạn đang xem tài liệu "Đề và đáp án thi chọn học sinh giỏi huyện Toán Lớp 6 - Năm học 2018-2019 - Phòng GD & ĐT Diễn Châ", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ THI CHỌN HỌC SINH GIỎI HUYỆN LỚP 6 NĂM HỌC 2018 – 2019 Môn: Toán – (Thời gian làm bài 120 phút) Câu 1 (4 điểm): Thực hiện phép tính (tính hợp lí nếu có thể) a) b) c) d) Câu 2 (4.5 điểm): Tìm x biết: a) b) c) 293 = 4. - 207 Câu 3 (4 điểm): a) Tìm hai số tự nhiên có tổng 432 và ƯCLN của chúng bằng 36. b) Tìm các số nguyên tố x, y sao cho x2 + 45 = y2 c) Tìm tất cả các số tự nhiên n để phân số rút gọn được. d) Tìm các số tự nhiên x và y sao cho Câu 4 (5.5 điểm): Cho góc xOy và góc yOz là hai góc kề bù. Biết góc yOz bằng năm lần góc yOx. a) Tính số đo mỗi góc. b) Gọi Ot là tia phân giác của góc yOz. Tính số đo góc xOt. c) Từ O vẽ tia Ot’ sao cho . Tính số đo góc zOt’. Câu 5 (2 điểm): Cho 40 điểm phân biệt trong đó có a điểm thẳng hàng, cứ qua 2 điểm ta vẽ được 1 đường thẳng. Tìm a, biết số đường thẳng tạo thành là 736 đường thẳng. -------------------------------------------Hết------------------------------------------- Giám thị không giải thích gì thêm Họ và tên thí sinh: .. SBD: .. HƯỚNG DẪN CHẤM THI MÔN TOÁN 6 Câu Nội dung Điểm Câu 1 (4đ) Thực hiện phép tính (Tính hợp lí nếu có thể) a) b) c) d) a) = 1 đ b) 1 đ c) 1 đ d) 1 đ Câu 2 (4.5đ) Tìm x biết: a) b) c) = d) 293 = 4. - 207 a) ó ó ó 0.25 đ 0.5 0.5 0.25 0.5 đ 0.5 đ 0.25 đ 0.25 đ c) 293 = 4. - 207 ó4.= 500 ó= 125 ó= 53 ó |x + 2|=3 +) x + 2 = 3 ó x = 1 +) x + 2 = - 3 ó x = - 5 0.25 đ 0.25 đ 0.5 đ 0.25 đ 0.25 đ Câu 3 (4đ) a) Tìm hai số tự nhiên có tổng 432 và ƯCLN của chúng bằng 36. b) Tìm số nguyên tố x, y sao cho x2 + 45 = y2 c) Tìm tất cả các số tự nhiên n để phân số rút gọn được. d) Tìm các số tự nhiên x và y sao cho a) Gọi hai số tự nhiên phải tìm là a và b . Ta có: ƯCLN(a,b) = 36 nên a = 36c và b = 36d, (c, d) = 1. Vì tổng của hai số bằng 432 nên a+b=432 => 36(c+d) = 432 => c + d = 12. Như vậy ta phải tìm các cặp số c, d có tổng bằng 12 và (c,d ) = 1. Các cặp số đó là 1 và 11; 5 và 7. Các số tự nhiên cần tìm là a = 36, b = 396 và a = 180, b = 252 hoặc ngược lại. 0.25 đ 0.25 đ 0.25 đ 0.25 đ b) Vì x, y là các số nguyên tố và x2 + 45 = y2 nên y2 > 45 => y 7 => y là số lẻ. Suy ra x2 phải là số chẵn và x nguyên tố => x = 2. Với x = 2 ta có 22 + 45 = y2 => y = 7 0.5 đ 0.25 đ 0.25 đ c) Giả sử tử số và mẫu số cùng chia hết cho số nguyên tố d. Khi đó ta có 7(6n + 2) – 2(21n + 6) d => 2d => d = 2. Ta luôn luôn có 6n + 2 chia hết cho 2, nên để A rút gọn được khi 21n + 6 cũng chia hết cho 2 ó n là số tự nhiên lẻ. 0.25 đ 0.25 đ 0.25 đ 0.25 đ d) = => y(5x – 3) = 60 Như vậy 5x – 3 là ước của 60 và tận cùng bằng 7 hoặc 2 do đó 5x – 3 bằng 2 hoặc 12. Tương ứng x = 1, y = 30 hoặc x = 3, y = 5. 0.25 đ 0.25 đ 0.25 đ 0.25 đ Câu 4 (5.5đ) Cho góc xOy và góc yOz là hai góc kề bù. Biết góc zOy bằng năm lần góc yOx. a) Tính số đo mỗi góc. b) Gọi Ot là tia phân giác của góc yOz. Tính số đo góc xOt. c) Từ O vẽ tia Ot’ sao cho . Tính số đo góc zOt’. 0.5 đ a)Vì góc xOy và góc yOz là hai góc kề bù nên: =1800 mà nên 6 = 1800 Do đó: = 1800:6 = 300 ; = 5.300 = 1500 0.5 đ 0.5 đ 0.5 đ b)Vì Ot là tia phân giác của góc nên = 750. Vì góc xOt và góc tOz là hai góc kề bù nên: =1800 Do đó = 1800- 750 = 1050 0.5 đ 0.5 đ 0.5 đ c) TH1: Tia Ot’ thuộc nửa mặt phẳng bờ Ot không chứa tia Oz => Tia Ot nằm giữa hai tia Oz và Ot’ => = TH2: Tia Ot’ thuộc nửa mặt phẳng bờ Ot chứa tia Oz => Hai tia Oz và Ot’ thuộc cùng một nửa mặt phẳng bờ chứa tia Ot, mà (750< 900) nên tia Oz nằm giữa hai tia Ot và Ot’ => 0.5 đ 0.5 đ 0.5 đ 0.5 đ Câu 5 (2đ) Cho 40 điểm phân biệt trong đó có a điểm thẳng hàng, cứ qua 2 điểm ta vẽ được 1 đường thẳng. Tìm a, biết số đường thẳng tạo thành là 736 đường thẳng. Giả sử trong 40 điểm phân biệt không có 3 điểm nào thẳng hàng + Chọn một điểm bất kì trong 40 điểm đã cho. Qua điểm đó và từng điểm trong 39 điểm còn lại ta vẽ được 39 đường thẳng. + Làm như vậy với 40 điểm thì ta vẽ được tất cả là 39.40 đường thẳng. + Nhưng mỗi đường thẳng đã được tính hai lần nên số đường thẳng thực tế vẽ được là đường thẳng. Vậy qua 40 điểm phân biệt mà không có 3 điểm nào thẳng hàng ta vẽ được 780 đường thẳng. – Tương tự như trên, giả sử trong a điểm phân biệt không có 3 điểm nào thẳng hàng ta vẽ được đường thẳng. Nhưng qua a điểm thẳng hàng ta chỉ vẽ được một đường thẳng nên số đường thẳng bị giảm đi là đường thẳng. Theo bài ra ta có : Vì a - 1 và a là hai số tự nhiên liên tiếp và nên 0.5 đ 0.5đ 0.5đ 0.5đ Chú ý: - Hướng dẫn chấm này có 03 trang, chấm theo thang điểm 20. - Học sinh giải cách khác đúng cho điểm tối đa. - Học sinh làm câu 4 không vẽ hình hoặc vẽ sai hình thì không chấm điểm
Tài liệu đính kèm:
 de_va_dap_an_thi_chon_hoc_sinh_gioi_huyen_toan_lop_6_nam_hoc.docx
de_va_dap_an_thi_chon_hoc_sinh_gioi_huyen_toan_lop_6_nam_hoc.docx



