Đề thi chọn học sinh giỏi huyện Toán Lớp 9 - Năm học 2016-2017 - Phòng GD & ĐT Tư Nghĩa

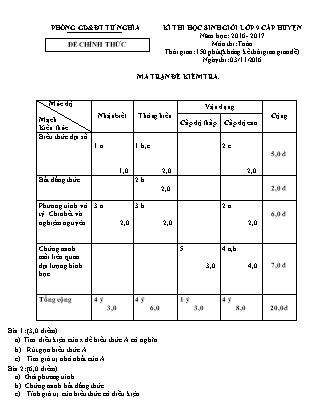
 PHÒNG GD&ĐT TƯ NGHĨA
ĐỀ CHÍNH THỨC
KÌ THI HỌC SINH GIỎI LỚP 9 CẤP HUYỆN
Năm học: 2016 - 2017
Môn thi: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 03/11/2016
 MA TRẬN ĐỀ KIỂM TRA.
 Mức độ
Mạch
Kiến thức 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Biểu thức đại số 
1.a
 1,0
1.b,c
 2,0
2.c
 2,0
5,0 đ
Bất đẳng thức 
2.b
 2,0
2,0 đ
Phương trình vô tỷ .Chia hết và nghiệm nguyên
3.a
 2,0
3.b
 2,0
2.a
 2,0
6,0 đ
Chứng minh mối liên quan đại lượng hình học 
5
 3,0
4.a,b
 4,0
7,0 đ
Tổng cộng
4 ý
3,0
4 ý
6,0
1 ý
3,0
4 ý
8,0
20,0đ
Bài 1: (3,0 điểm).
Tìm điều kiện của x để biểu thức A có nghĩa .
Rút gọn biểu thức A .
Tìm giá trị nhỏ nhất của A.
Bài 2: (6,0 điểm).
Giải phương trình
Chứng minh bất đẳng thức 
 Tính giá trị của biểu thức có điều kiện 
Bài 3: (4,0 điểm).
Chứng minh chia hết 
Tìm các số nguyên x,y thỏa mãn cho trước 
Bài 4: (4,0 điểm).
Chứng minh về diện tích 
Chứng minh đẳng thức hình học 
Bài 5: (3,0 điểm).
 Tính diện tích hình học 
 PHÒNG GD&ĐT TƯ NGHĨA 
ĐỀ CHÍNH THỨC
KÌ THI HỌC SINH GIỎI LỚP 9 CẤP HUYỆN
Năm học: 2016 - 2017
Môn thi: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 03/11/2016
Bài 1:(3 điểm)
Cho biểu thức 
a) Tìm điều kiện của x để biểu thức A có nghĩa .
b)Rút gọn biểu thức A .
 c)Tìm giá trị nhỏ nhất của A.
Bài 2:(6 điểm) 
a)Giải phương trình: .
 b)Chứng minh rằng : biết x3 + y3 + 3(x2+y2) + 4(x+ y) + 4 = 0 và x.y > 0. 
c)Cho thỏa mãn . 
Tính giá trị của biểu thức .
Bài 3:(4 điểm)
a)Với n chẵn (nN) chứng minh rằng: (20n + 16n – 3n – 1)323
b)Tìm các số nguyên x,y thỏa mãn : 
Bài 4:(4 điểm) 
Cho tam giác ABC ( có ba góc nhọn) nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF cắt nhau tại H. Kéo dài AO cắt đường tròn tại K. Gọi G là trọng tâm của tam giác ABC. 
a) Chứng minh SAHG = 2SAGO
b) Chứng minh 
Bài 5:(3 điểm) 
Cho nửa đường tròn (O; R) đường kính AB. C và D là hai điểm nằm trên nửa đường tròn đó sao cho góc , góc . AC cắt BD tại M. Tính diện tích tam giác ABM theo R
..........................HẾT.............................
PHÒNG GD&ĐT TƯ NGHĨA
ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN
Đề thi học sinh giỏi lớp 9 cấp trường 
Năm học: 2016 - 2017
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 22/10/2016
Bài
Nội dung 
Điểm
1a
(1đ)
a) Điều kiện của x để biểu thức A có nghĩa :
1,0đ
1b
(1đ)
b) Rút gọn biểu thức A 
1,0đ
 1c
(1đ)
 Tìm giá trị nhỏ nhất của A.
Ta có 
Ta có A nhỏ nhất khi đạt giá trị nhỏ nhất 
Vậy: Giá trị nhỏ nhất của là A là khi = 0
1,0đ
2a
(2đ)
Giải phương trình: 
Điều kiện 
ÞPhương trình đã cho tương đương với
1,0đ
 (thỏa mãn điều kiện)
Vậy là nghiệm của phương trình đã cho.
1,0đ
2b
(2đ)
Chứng minh: biết x3 + y3 + 3(x2+y2) + 4(x+ y) + 4 = 0 và x.y > 0. 
Ta có: x3 + y3 + 3(x2+y2) + 4(x+ y) + 4 = 0
 (x + y)( x2 – xy + y2) + 2(x2 – xy + y2) + (x2 + 2xy + y2) + 4(x+y) + 4 = 0
 ( x2 – xy + y2)( x + y + 2) + ( x + y + 2)2 = 0
 ( x + y + 2)( x2 – xy + y2 + x + y + 2) = 0
.( x + y + 2)( 2x2 – 2xy + 2y2 + 2x + 2y + 4) = 0
.( x + y + 2).= 0
 x + y + 2 = 0
 x + y = -2 mà x.y > 0 nên x< 0, y < 0
1,0đ
Áp dụng BĐT CauChy ta có 
Do đó xy 1 suy ra 1 hay -2 Mà 
Vậy (đpcm)
1,0đ
2c
(2đ)
Cho thỏa mãn . 
Tính giá trị của biểu thức 
Ta có: 
(yz + xz + xy)(x + y + z) = xyz
xyz + zy2 + yz2 + zx2 + xyz + xz2 + yx2 + xy2 + xyz = xyz
(xyz + zx2 + xy2+ yx2)+ (zy2 + yz2 + xz2 + xyz) = 0
 1,0đ
x(yz + zx + y2+ yx)+ z(y2 + yz + xz + xy) = 0 
(yz + zx + y2+ yx)( x+ z) = 0 
 Thay vào B tính được B = 0
1,0đ
3a
(2đ)
Với n chẵn (nN) chứng minh rằng: 20n + 16n – 3n – 1323
Ta có: 323=17.19
20n + 16n – 3n – 1= (20n – 1) + (16n – 3n)
20n – 119
16n – 3n19 (n chẵn)
Do đó 20n + 16n – 3n – 119 (1)
1,0đ
20n + 16n – 3n – 1= (20n – 3n) + (16n –1)
20n – 3n 17
16n –1n17 ( n chẵn)
Do đó 20n + 16n – 3n – 117 (2)
Mà (17;19) = 1 nên từ (1) và (2) suy ra 20n + 16n – 3n – 1323 
1,0đ
3b
(2đ)
b) Tìm các số nguyên x,y thỏa mãn : 
Nếu y+2=0 lúc đó phương trình có dạng (vô nghiệm ).
Nếu thì ta có 
 1,0đ
Vì x,y nguyên nên nguyên Ư(1) .
Với (loại ).
Với .
Vậy số nguyên x,y thỏa mãn đề bài là : x=0,y=-1
1,0đ
4
(4đ)
5
(3đ)
Chứng minh SAHG = 2SAGO 
Tam giác ACK nội tiếp đường tròn (O) đường kính AK 
Nên KC vuông góc với AC
Mà BE vuông góc với AC (gt)
Suy ra KC // BE hay KC // BH
Chứng minh tương tự ta có KB // CH 
Nên tứ giác BHCK là hình bình hành
Gọi M giao điểm của BC và HK nên
M là trung điểm của BC mà G là trọng tâm của tam giác ABC nên AG = AM
M là trung điểm của HK nên AM là đường trung tuyến của tam giác AHK. 
Mà G thuộc đoạn AM và AG = AM nên G là trọng tâm của tam giác AHK
Ta có O là trung điểm của AK nên HO là đường trung tuyến của tam giác AHK 
Nên HO đi qua G do đó HG = 2GO
Tam giác AHG và tam giác AGO có chung đường cao kẻ từ A đến HO và HG = 2GO
Do đó SAHG = 2SAGO
Chứng minh 
 Ta có: = = 1
Tính diện tích tam giác ABM theo R
 1,0đ
1,0đ
2,0đ
Gọi N là giao điểm của AD và BC; H là giao điểm của MN và AB
 Chứng minh góc; mà góc (gt) nên tam giác vuông cân
MH = AH
MH + HB = AH + HB = 2R (1)
1,0đ
* Tam giác vuông tại H
HB=MB.cos MBH 
MH= MB.sinMBH MH HB= (2)
Từ (1) và (2) ta có MH + 
Vậy: 
2,0đ
Chú ý: 
-Học sinh có thể giải theo cách khác, nếu đúng vẫn cho điểm tối đa.
-Không có điểm vẽ hình.
-Chứng minh mà không có hình vẽ hoặc hình vẽ sai thì không có điểm.
Duyệt đề: Nghĩa Thắng, ngày 01 tháng 11 năm 2016
 Giáo viên ra đề 
 Trương Quang An