Giáo án Hình học Lớp 8 - Bài 1: Đa giác. Đa giác đều

Chương
2
ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
Bài 1. ĐA GIÁC. ĐA GIÁC ĐỀU
A. KIẾN THỨC TRỌNG TÂM
1. Khái niệm về đa giác
Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
Đa giác có đỉnh được gọi là hình giác hay hình cạnh.
Với ta quen gọi là tam giác, tứ giác, ngũ giác, lục giác và bát giác.
Với ta gọi là hình 7 cạnh, hình 9 cạnh, hình 10 cạnh, 
Tổng độ lớn của các góc trong đa giác là (với là số đỉnh của đa giác).
2. Đa giác đều
Đa giác đều là đa giác có tất cả các cạnh và tất cả các góc bằng nhau.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
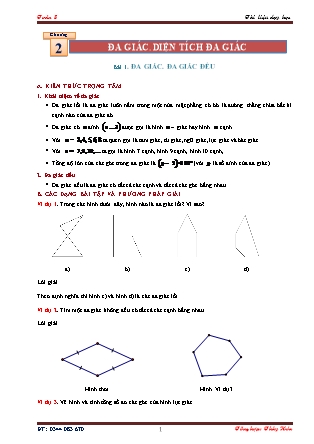
Ví dụ 1. Trong các hình dưới đây, hình nào là đa giác lồi? Vì sao?
	a)	b)	c)	d)
Lời giải
Theo định nghĩa thì hình c) và hình d) là các đa giác lồi.
Ví dụ 2. Tìm một đa giác không đều có tất cả các cạnh bằng nhau.
Lời giải
	Hình thoi	Hình Ví dụ 3
Ví dụ 3. Vẽ hình và tính tổng số đo các góc của hình lục giác.
Lời giải
Tổng độ lớn của các góc trong lục giác là
.
Ví dụ 4. Cho hình thoi có . Gọi , , , lần lượt là trung điểm của các cạnh , , , . Chứng minh đa giác là lục giác đều.
Lời giải
Dùng tính chất đường trung bình ta có
Ta có , là các tam giác cân có một góc bằng nên , là hai tam giác đều, từ đóLại có, theo tính chất trung bình,ta có:
 (góc ngoài tam giác) và , từ đó tính được Vậy là lục giác đều.
C. BÀI TẬP VẬN DỤNG
Bài 1: Tìm hình là đa giác lồi trong các hình dưới đây
	a)	b)	c)	d)
Bài 2. Vẽ hình và tính số đường chéo của ngũ giác, lục giác. \dapso{; }
Lời giải
Ngũ giác có đường chéo. 
Lục giác có đường chéo.
	Ngũ giác đều	Lục giác đều
Bài 3. Cho tam giác đều . Gọi , , lần lượt là trung điểm của các cạnh , , . Chứng minh là tam giác đều.
Lời giải
Trong tam giác có là đường trung bình nên .
Dùng tính chất đường trung bình chứng minh tương tự, ta được nên đều.
Bài 4. [*] Chứng minh hình -giác có tất cả đường chéo.
Lời giải
Từ mỗi đỉnh của hình -giác vẽ được đoạn thẳng nối đỉnh đó với đỉnh còn lại, trong đó có hai đoạn thẳng trùng với hai cạnh của đa giác. Do đó qua mỗi đỉnh của hình -giác vẽ được đường chéo. Hình -giác có đỉnh nên vẽ được đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy, hình -giác có tất cả đường chéo.
D. BÀI TẬP VỀ NHÀ
Bài 5. Vẽ các hình tứ giác lồi, ngũ giác lồi, lục giác lồi.
Lời giải
	Tứ giác lồi	Ngũ giác lồi	Lục giác lồi
Bài 6. Tìm một đa giác không đều có tất cả các góc bằng nhau.
Lời giải
Hình chữ nhật
Bài 7. Tính số đo mỗi góc của hình lục giác đều.
Lời giải
Đa giác đều có tất cả các góc bằng nhau, dùng kết quả bài trên ta tính được số đo mỗi góc của hình lục giác đều là .
Bài 8. Cho hình vuông . Gọi , , , lần lượt là trung điểm của các cạnh , , , . Chứng minh là hình vuông (tứ giác đều).
Lời giải
Do nên dùng tính chất đường trung bình của tam giác suy ra . 
Lại có, , , nên . Vậy là hình vuông.
--- HẾT ---