Giáo án Hình học Lớp 8 - Chương 1: Tứ giác - Vi Văn Yến
I. MỤC TIÊU
1.Kiến thức: - Nắm được định nghĩa hình thang, hình thang vuông, các yếu tố của hình thang. Biết cách chứng minh một tứ giác là hình thang, hình thang vuông.
2.Kỹ năng: - Biết về hình thang, hình thang vuông
- Biết tính số đo của hình thang, hình thang vuông.
3.Thái độ: - Nhanh nhẹn, linh hoạt trong việc nhận dạng hình thang, hình thang vuông.
II. CHUẨN BỊ:
1. Chuẩn bị của gv: Bảng phụ, thước êke
2. Chuẩn bị của hs: Nháp ,thước thẳng, êke.
III. TIẾN TRÌNH BÀI DẠY
1.Ổn định (1ph)
2.Kiểm tra bài cũ: (5ph)
HS1: Định nghĩa tứ giác, tứ giác lồi, các đặc điểm của tứ giác.
HS2: Số đo tổng các góc trong tứ giác,chữa BT3(sgk)
3. Bài mới:
1) Đặt vấn đề vào bài: 2ph
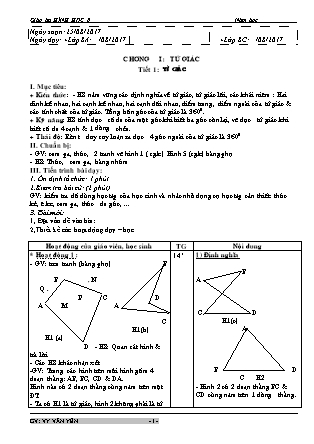
GV đưa hình ảnh bên lên bảng cho HS nhận xét
tứ giác bên có gì đặc biệt.
HS: Có hai cạnh AB và CD song song
GV: Vậy tứ giác như vậy gọi là gì? nó có đặc điểm,
tính chất như thế nào ? Đó là nội dung bài học hôm nay.
2) Thiết kế các hoạt động dạy – học
Ngày soạn: 25/08/2017 Ngày dạy: +Lớp 8A: /08/2017 +Lớp 8C: /08/2017 Ch¬ng I: Tø gi¸c Tiết 1: Tø gi¸c I. Mục tiêu: + KiÕn thøc: - HS n¾m v÷ng c¸c ®Þnh nghÜa vÒ tø gi¸c, tø gi¸c låi, c¸c kh¸i niÖm : Hai ®Ønh kÒ nhau, hai c¹nh kÒ nhau, hai c¹nh ®èi nhau, ®iÓm trong, ®iÓm ngoµi cña tø gi¸c & c¸c tÝnh chÊt cña tø gi¸c. Tæng bèn gãc cña tø gi¸c lµ 3600. + Kü n¨ng: HS tÝnh ®îc sè ®o cña mét gãc khi biÕt ba gãc cßn l¹i, vÏ ®îc tø gi¸c khi biÕt sè ®o 4 c¹nh & 1 ®êng chÐo. + Th¸i ®é: RÌn t duy suy luËn ra ®îc 4 gãc ngoµi cña tø gi¸c lµ 3600 II. Chuẩn bị: - GV: com pa, thíc, 2 tranh vÏ h×nh 1 ( sgk ) H×nh 5 (sgk) b¶ng phô - HS: Thíc, com pa, b¶ng nhãm III. Tiến trình bài dạy: 1. Ổn định tổ chức: 1 phút 2.Kiểm tra bài cũ: (2 phút) GV: kiÓm tra ®å dïng häc tËp cña häc sinh vµ nh¾c nhë dông cô häc tËp cÇn thiÕt: thíc kÎ, ª ke, com pa, thíc ®o gãc, ... 3. Bài mới: 1, Đặt vấn đề vào bài: 2,Thiết kế các hoạt động dạy – học . Ho¹t ®éng cña gi¸o viªn, häc sinh TG Néi dung * Ho¹t ®éng 1: - GV: treo tranh (b¶ng phô) B B . N Q . P C D A M A C H1(b) H1 (a) D - HS: Quan s¸t h×nh & tr¶ lêi - C¸c HS kh¸c nhËn xÐt -GV: Trong c¸c h×nh trªn mçi h×nh gåm 4 ®o¹n th¼ng: AB, BC, CD & DA. H×nh nµo cã 2 ®o¹n th¼ng cïng n»m trªn mét §T - Ta cã H1 lµ tø gi¸c, h×nh 2 kh«ng ph¶i lµ tø gi¸c. VËy tø gi¸c lµ g× ? - GV: Chèt l¹i & ghi ®Þnh nghÜa - GV: gi¶i thÝch : 4 ®o¹n th¼ng AB, BC, CD, DA trong ®ã ®o¹n ®Çu cña ®o¹n th¼ng thø nhÊt trïng víi ®iÓm cuèi cña ®o¹n th¼ng thø 4. + 4 ®o¹n th¼ng AB, BC, CD, DA trong ®ã kh«ng cã bÊt cø 2 ®o¹n th¼ng nµo cïng n»m trªn 1 ®êng th¼ng. + C¸ch ®äc tªn tø gi¸c ph¶i ®äc hoÆc viÕt theo thø tù c¸c ®o¹n th¼ng nh: ABCD, BCDA, ADBC +C¸c ®iÓm A, B, C, D gäi lµ c¸c ®Ønh cña tø gi¸c. + C¸c ®o¹n th¼ng AB, BC, CD, DA gäi lµ c¸c c¹nh cña tø gi¸c. * Ho¹t ®éng 2: -GV: H·y lÊy mÐp thíc kÎ lÇn lît ®Æt trïng lªn mçi c¹ch cña tø gi¸c ë H1 råi quan s¸t - H1(a) lu«n cã hiÖn tîng g× x¶y ra ? - H1(b) (c) cã hiÖn tîng g× x¶y ra ? - GV: BÊt cø ®¬ng th¼ng nµo chøa 1 c¹nh cña h×nh H1(a) còng kh«ng ph©n chia tø gi¸c thµnh 2 phÇn n»m ë 2 nöa mÆt ph¼ng cã bê lµ ®êng th¼ng ®ã gäi lµ tø gi¸c låi. - VËy tø gi¸c låi lµ tø gi¸c nh thÕ nµo ? + Trêng hîp H1(b) & H1 (c) kh«ng ph¶i lµ tø gi¸c låi * Ho¹t ®éng 3: GV: VÏ H3 vµ gi¶i thÝch kh¸i niÖm: GV: Kh«ng cÇn tÝnh sè mçi gãc h·y tÝnh tæng 4 gãc + == ? (®é) - Gv: ( gîi ý hái) + Tæng 3 gãc cña 1 lµ bao nhiªu ®é? + Muèn tÝnh tæng + = ? (®é) ( mµ kh«ng cÇn ®o tõng gãc ) ta lµm ntn? + Gv chèt l¹i c¸ch lµm: - Chia tø gi¸c thµnh 2 cã c¹nh lµ ®êng chÐo - Tæng 4 gãc tø gi¸c = tæng c¸c gãc cña 2 ABC & ADC Tæng c¸c gãc cña tø gi¸c b»ng 3600 - GV: VÏ h×nh & ghi b¶ng 14’ 5’ 13’ 1) §Þnh nghÜa B A C D H1(c) A B ‘ D C H2 - H×nh 2 cã 2 ®o¹n th¼ng BC & CD cïng n»m trªn 1 ®êng th¼ng. * §Þnh nghÜa: Tø gi¸c ABCD lµ h×nh gåm 4 ®o¹n th¼ng AB, BC, CD, DA trong ®ã bÊt kú 2 ®o¹n th¼ng nµo còng kh«ng cïng n»m trªn mét ®êng th¼ng. * Tªn tø gi¸c ph¶i ®îc ®äc hoÆc viÕt theo thø tù cña c¸c ®Ønh. * §Þnh nghÜa tø gi¸c låi * §Þnh nghÜa: (sgk) * Chó ý: Khi nãi ®Õn 1 tø gi¸c mµ kh«ng gi¶i thÝch g× thªm ta hiÓu ®ã lµ tø gi¸c låi + Hai ®Ønh thuéc cïng mét c¹nh gäi lµ hai ®Ønh kÒ nhau + hai ®Ønh kh«ng kÒ nhau gäi lµ hai ®Ønh ®èi nhau + Hai c¹nh cïng xuÊt ph¸t tõ mét ®Ønh gäi lµ hai c¹nh kÒ nhau + Hai c¹nh kh«ng kÒ nhau gäi lµ hai c¹nh ®èi nhau - §iÓm n»m trong M, P ®iÓm n»m ngoµi N, Q 2/ Tæng c¸c gãc cña mét tø gi¸c ( HD4) B 1 A 1 2 C 2 D + + = 1800 + + = 1800 nên + = 3600 * §Þnh lý: SGK 4.Củng cố dặn dò: 10 phút + Củng cố: - GV: cho HS lµm bµi tËp trang 66. H·y tÝnh c¸c gãc cßn l¹i + Dặn dò: - Nªu sù kh¸c nhau gi÷a tø gi¸c låi & tø gi¸c kh«ng ph¶i lµ tø gi¸c låi ? - Lµm c¸c bµi tËp : 2, 3, 4 (sgk) * Bµi tËp NC: ( Bµi 2 sæ tay to¸n häc) Cho tø gi¸c låi ABCD chøng minh r»ng: ®o¹n th¼ng MN nèi trung ®iÓm cña 2 c¹nh ®èi diÖn nhá h¬n hoÆc b»ng nöa tæng 2 c¹nh cßn l¹in(Gîi ý: Nèi trung ®iÓm ®êng chÐo). - §äc tríc § 2 H×nh Thang Ngày soạn: 25/08/2017 Ngày dạy: +Lớp 8A: /08/2017 +Lớp 8C: /08/2017 Tiết 2: HÌNH THANG I. MỤC TIÊU 1.Kiến thức: - Nắm được định nghĩa hình thang, hình thang vuông, các yếu tố của hình thang. Biết cách chứng minh một tứ giác là hình thang, hình thang vuông. 2.Kỹ năng: - Biết về hình thang, hình thang vuông - Biết tính số đo của hình thang, hình thang vuông. 3.Thái độ: - Nhanh nhẹn, linh hoạt trong việc nhận dạng hình thang, hình thang vuông. II. CHUẨN BỊ: 1. Chuẩn bị của gv: Bảng phụ, thước êke 2. Chuẩn bị của hs: Nháp ,thước thẳng, êke. III. TIẾN TRÌNH BÀI DẠY 1.Ổn định (1ph) 2.Kiểm tra bài cũ: (5ph) HS1: Định nghĩa tứ giác, tứ giác lồi, các đặc điểm của tứ giác. HS2: Số đo tổng các góc trong tứ giác,chữa BT3(sgk) 110o 70o A B C A 3. Bài mới: 1) Đặt vấn đề vào bài: 2ph GV đưa hình ảnh bên lên bảng cho HS nhận xét tứ giác bên có gì đặc biệt. HS: Có hai cạnh AB và CD song song GV: Vậy tứ giác như vậy gọi là gì? nó có đặc điểm, tính chất như thế nào ? Đó là nội dung bài học hôm nay. 2) Thiết kế các hoạt động dạy – học Các hoạt động của thầy và trò TG Nội dung 1.Hoạt động1: GV: Quay lại bài cũ. Tứ giác có tính chất như ở trên gọi là hình thang. Vậy hình thang là hình như thế nào ? HS: Phát biểu định nghĩa như Sgk. GV:Giới thiệu các đặc điểm của hình thang. [?1]Cho các hình sau : E A D B C G H F I N M K (a) (b) (c ) 60o 60o 150o 75o 75o 115o a) Tìm các tứ giác là hình thang. b) Có nhận xét gì về hai góc kề một cạnh bên của hình thang? Hs: Hoạt động nhóm làm vào giấy nháp gv đã soạn sẵn GV: Thu phiếu và cùng cả lớp kiểm tra lại. GV: Đưa đề bài tập ?2 lên bảng phụ. HS: Hai học sinh lên bảng thực hiện. Học sinh ở dưới làm vào vở. GV:Hướng dẩn -Muốn chứng minh các đoạn thẳng bằng nhau ta thường chứng minh điều gì ? -Muốn c/m hai đoạn thẳng song song ta phải c/m gì? HS: Nhận xét kết quả của các bạn. GV: Qua bài tập trên em rút ra cho mình được điều gì về các cạnh bên và cạnh đáy bằng nhau. HS: Phát biểu nhận xét trong sgk. 2.Hoạt động2: GV:Em có nhận xét gì về hình thang trên ? HS: Có góc A bằng 90o. GV: Ta nói ABCD là hình thang vuông.Vậy hình thang vuông là hình như thế nào? HS: Phát biểu định nghĩa trong sgk. GV: Đưa tranh vẽ hình 20 lên bảng cho học sinh thực hiện. HS: Làm bài tập 6 trong sgk theo hướng dẫn. 15’ 15’ 1. Định nghĩa: (SGK) C A B D H * AB và CD là đáy. *AD và BC là hai cạnh bên. * AH là đường cao. ?1 a) Các tứ giác ABCD,EFGH là hình thang. b) Hai góc kề một cạnh bên của hình thang bù nhau. 1 2 2 1 A B C D ?2. a) Xét 2 tam giác ABC và CDA có: A1 = C1 AC chung. A2 = C2 Þ DABC = DCDA(g.c.g) 1 1 A B C D Þ AB = DC và AD = BC b) Xét 2 tam giác ABC và CDA có: A1 = C1 AC chung. AB = CD (gt) => D ABC = D CDA(c.g.c) => AD = BC và AD // BC( vì có cặp góc so le trong bằng nhau) * Nhận xét: (sgk) 2. Hình thang vuông. * Định nghĩa: (sgk) BT6:Hình a) và c) là hình thang. 4. Củng cố -Dặn dò + Củng cố: (6ph) - Nhắc lại định nghĩa hình thang, các đặc điểm của hình thang. - Định nghĩa hình thang vuông. - Cách tính các góc của hình thang. * Chọn câu trả lời đúng trong các câu sau: A.Hình thang có ba góc tù một góc nhọn. B.Hình thang có ba góc vuông một góc nhọn. C.Hình thang có nhiều nhất hai góc tù, nhiều nhất hai góc nhọn. D.Hình thang có ba góc nhọn, một góc tù. +Nhiệm vụ về nhà: (1ph) - Học thuộc các định nghĩa, đặc điểm của hình thang, hình thang vuông. - Làm bài tập 8,9 (sgk) Ngày soạn: 03/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 3: HÌNH THANG CÂN I MỤC TIÊU. 1.Kiến thức : - Nắm được định nghĩa, các tính chất, dấu hiệu nhận biết hình thang cân 2.Kỷ năng: - Biết vận dụng định nghĩa, các tính chất của hình thang cân trong việc nhận dạng và chứng minh được các bài toán có liên quan đến hình thang cân. - Rèn thao tác phân tích qua việc phán đoán, chứng minh. 3.Thái độ: - Rèn đức tính cẩn thận, chính xác trong lập luận chứng minh. Nêu vấn đề, trực quan, nhóm. II. CHUẨN BỊ Chuẩn bị của gv: Bảng phụ, bút dạ, thước đo góc. Chuẩn bị của hs: Bút dạ, thước thẳng, xem lại bài cũ. III. TIẾN TRÌNH BÀI DẠY 1.Ổn định: (1ph) 2.Kiểm tra bài cũ: (7 ph) HS1: Phát biểu định nghĩa hình thang, hình thang vuông, tổng các góc trong của hình thang. HS2: Chửa bài tập 9 GV: Đưa thêm. Cho thêm hai góc ABC và DCB bằng nhau. So sánh AC và BD? nhận xét gì về hai góc BAD và CDA. 3. Bài mới: 1) Đặt vấn đề.(1ph) Vậy hình thang có các tính chất như trên còn gọi là hình gì ? Có tính chất như thế nào? Đó là nội dung bài học hôm nay. 2) Thiết kế các hoạt động dạy và học Hoạt động của thầy và trò TG Nội dung 1. Hoạt động 1: GV: Hình thang có tính chất như vậy gọi là hình thang cân. Vậy hình thang cân là hình như thế nào? HS: phát biểu định nghiã trong Sgk. GV: Nêu chú ý cho học sinh. GV:Đưa bài [?2] lên bảng phụ, phát phiếu học tập cho học sinh. Cho các hình sau: B A D C E F G H I K M N T S P Q 800 800 1000 800 800 1100 700 1100 700 c) d) a) b) a) Tìm các hình thang cân. b) Tính các góc còn lại của hình thang cân đó. c) Có nhận xét gì về hai góc đối của hình thang cân. HS: Hoạt động theo nhóm trên giấy trong Gv đã soạn sẳn. GV: Thu phiếu của các nhóm đưa lên đèn chiếu cho Hs nhận xét kết quả của nhau.GV chốt lại và nhấn mạnh các ý trên. 15’ A B C D 1. Định nghĩa: (Sgk) Tứ giác ABCD là hình thang cân(đáy AB, CD) AB // CD A = D hoặc A = B 2 a) Hình a),c) và d) là hình thang cân. b) D = 1000, N = 700, I = 1100, S = 900 c) Hai góc đối của hình thang cân có tổng số đo là 1800. 2. Hoạt động 2: GV: Quay lại phần bài cũ trong câu so sánh hai cạnh AD và BC,Vậy hình thang cân có hai cạnh bên như thế nào với nhau? HS: Đọc định lí trong Sgk. GV: Phần chứng minh định lý đó các em đã được làm ở phần bài tập, GV chỉ nói qua trong trường hợp hai cạnh bên song. GV: Cho học sinh nhận xét hai đường chéo của hình thang cân. HS: Hình thang cân có hai đường chéo bằng nhau. GV: Để chứng minh điều này ta làm thế nào? GV vẽ hình lên bảng. HS: Phân tích và chứng minh dưới lớp, một em lên bảng trình bày. GV: Cùng học sinh nhận xét bài làm và chốt lại. GV: Trong hình thang thì có hai đường chéo bằng nhau.Vậy nếu tứ giác có hai đường chéo bằng nhau có là hình thang hay không? HS: Trả lời và làm [?3] sau đó nêu định lí 3. 3.Hoạt động 3: GV: Qua các quá trình trên vậy em nào cho biết làm thế nào để nhận biết một tứ giác là hình thang cân. HS: Phát biểu dấu hiệu SGK 12’ 5’ 2. Tính chất: * Định lí 1: (Sgk) A B C D *Chú ý. Có những hình thang có hai cạng bên bằng nhau nhưng không là hình thang cân. *Định lí 2: (Sgk) GT ABCD là hình thang cân (AB // CD) KL AC = BD Chứng minh: Xét D ADC và DBCD có: CD (cạnh chung) ADC = BCD (định nghĩa) AD = BC ( định lí 1) nên D ADC = DBCD (c.g.c) Vậy AC = BD. * Định lí 3: 3) Dấu hiệu nhận biết (SGK) 4. Củng cố- Dặn dò + Củng cố: 2ph - Điền ký hiệu “ Đ ” hoặc “S ” vào ô vuông trong các mệnh đề sau: Hình thang có hai đường chéo bằng nhau là hình thang cân . Hình thang cân là hình thang có hai đường chéo bằng nhau. + Nhiệm vụ về nhà : 2ph - Học bài theo SGK. Làm các bài tập 12;13;14 Tiết sau luyện tập. Ngày soạn: 03/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 4: LUYỆN TẬP I.Môc tiªu *KT:-Hs ®îc kh¾c s©u vÒ h×nh thang, htc (§n, tc, c¸ch nhËn biÕt) *KN:-RÌn luyÖn kÜ n¨ng vµ t duy h×nh häc trong c¸c bµi tËp h×nh thang ,tÝnh ch¸t cña h×nh thang .nhËn biÕt h×nh thang c©n. *T§: RÌn tÝnh cÈn thËn , chÝnh x¸c trong h×nh häc II.ChuÈn bÞ -Gi¸o viªn: Thíc th¼ng, compa, b¶ng phô, phÊn mµu . -Hs: Thíc th¼ng, häc bµi cò. III. TiÕn tr×nh bµi d¹y 1.æn ®Þnh líp(1) 2.KiÓm tra bµi cò (7) ?HS1: Nªu §N , tÝnh chÊt cña h×nh thang c©n, H·y vÏ h×nh thang cã hai c¹nh bªn b»ng nhau nhng kh«ng ph¶i lµ h×nh thang c©n ?HS 2:Nªu dÊu hiÖu nhËn biÕt htc. Cho htc ABCD, kÎ hai ®êng chÐo AC, BD. H·y dïng c¸c kÝ hiÖu vÒ ®o¹n th¼ng b»ng nhau, cÆp gãc b»ng nhau ®Ó ®¸nh dÊu c¸c cÆp c¹nh vµ cÆp gãc b»ng nhau. 3. Bµi míi 3.1 Đặt vấn đề 3.2. thiết kế hoạt động dạy-học Ho¹t ®éng cña thµy vµ trß Tg Néi dung *H§1:Ch÷a bµi 12 (sgk-t74) -Hs: §äc ®Ò, vÏ h×nh, ghi GT,KL -Gv: Yªu cÇu 1 hs lªn b¶ng, díi líp lµm vµo vë. -Hs: NhËn xÐt. -Gv: ChØnh söa. Gv: Lu ý khi bµi to¸n yªu cÇu cm hai ®o¹n th¼ng b»ng nhau, thêng ta ®i cm hai tam gi¸c b»ng nhau. *H§2: Bµi 13 (SGK-T74) -Hs ®äc ®Ò, vÏ h×nh, ghi gt, kl -Gv: Yªu cÇu hs suy nghÜ, cm -Hs lªn b¶ng tr×nh bµy Hs: NhËn xÐt -Gv: ChØnh söa *H§3: Bµi 15 (sgk-t75) -Hs ®äc bµi, vÏ hinh, ghi gt,kl -hs suy nghÜ t×m c¸ch cm -Hs: Tr¶ lêi miÖng -Hs: NhËn xÐt -Gv: ghi b¶ng *H§4: Bµi 16(sgk-t75) -H/s vÏ h×nh ,ghi gi¶ thiÕt ,kÕt luËn -§Ó cm EDCB lµ htc ta cÇn cm ®iÒu g×? -Hs: Ta cÇn cm EB=DC -gv: Em h·y so s¸nh víi bµi 15 -Hs: Hai bµi nµy t¬ng tù nhau , do ®ã ta cÇn cm AE=AD -Gv: Yªu cÇu hs suy nghÜ vµ tr¶ lêi miÖng c¸ch cm 6 7 10 9 Bµi 12 (sgk-t74) Cho htc ABCD (AB//CD; AB<CD) GT AECD; BF CD KL DE=CF CM: XÐt AED vµ BFC ta cã (v× ABCD lµ htc) ; AD=BC (c¹nh bªn cña htc) (c¹nh huyÒn-gãc nhän) DC=CF (§PCM) Bµi 13 Cho htc ABCD (AB//CD); GT AC c¾t BD t¹i E KL EA=EB; EC=ED Cm XÐt vµ BDC cã AD=BC (tc cña htc) (§n htc) DC chung (c.g.c) MµEDC c©n t¹i E ED=EC Ta l¹i cã AC=BDAC-EC=BD-DE AE=BE Bµi 15 Cm: a)Ta cã ADE c©n gãc D1= gãc E1 gãc D2= gãc E2 Mµ (1) Do ABC c©n (gt) (2) Tõ (1) vµ (2) ,ta kl tø gi¸c AECB lµ h×nh thang c©n b) do Bµi 16 GT ABC c©n t¹i A,? KL BEDClµ ht c©n cã hai c¹nh bªn ABD=ACE(c,g,c) AD=AE; BD=EC cm BEDC lµ ht c©n ( nh bµi 15) MÆt kh¸c: DE//BC gãcD1= gãc B2 gãcB1= gãcD1 do®ã DEB c©n DE=BE 4. Cñng cè- Dặn dò (5’) * Cñng cè (3) Hs nh¾c l¹i ®n, tc, dÊu hiÖu nhËn biÕt ht, htc * Dặn dò (2) -VÒ nhµ lam nh÷ng bµi tËp cßn l¹i - §äc tríc tݪt 5 ======================================================= Ngày soạn: 03/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 5: ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC, CỦA HÌNH THANG I. MỤC TIÊU 1. Kiến thức : - Nắm được định nghĩa về đường trung bình của tam giác, nội dung định lí1, định lí2. 2. Kỷ năng: - Biết vẽ đường trung bình của tam giác, vận dụng định lí 1, định lí 2 để tính độ dài các đoạn thẳng. 3. Thái độ: - Rèn đức tính cẩn thận, chính xác trong lập luận chứng minh. II. CHUẨN BỊ 1. Chuẩn bị của gv: Bảng phụ, bút dạ, thước đo góc. 2. Chuẩn bị của hs: Bút dạ, thước thẳng, xem lại bài cũ. III.TIẾN TRÌNH BÀI DẠY 1. Ổn định (1ph) 2. Kiểm tra bài cũ (5ph) Nêu dấu hiệu nhận biết hình thang cân ? 3. Bài mới: 1) Đặt vấn đề vào bài.(2ph) Giữa hai điểm B và C có chướng ngại vật . Biết DE = 50m, ta có thể tính được khoảng cách giữa hai điểm B và C . 2) Thiết kế các hoạt động dạy – học Ho¹t ®éng cña GV và HS TG Néi dung kiÕn thøc 1.Hoạt động1: Tìm hiểu định nghĩa GV: Cho học sinh thực hiện ?1 ở SGK GV: Bằng quan sát hãy nêu dự đoán về vị trí của điểm E trên AC ? HS: Dự đoán E là trung điểm của AC. GV: Đưa bài toán dưới dạng GT, KL cho HS. GT DABC, AD = DB, DE // BC KL AE = EC GV: Hướng dẫn HS chứng minh bài toán trên bằng cách đưa ra các câu hỏi gợi mở. Nêu nhận xét về hình thang có hai cạnh bên song song? HS: Hình thang có hai cạnh bên song song thì hai cạnh bên song song, hai cạnh đáy bằng nhau. GV: Hình thang DEFB có DB như thế nào với EF? Vì sao? HS: DB = EF GV: Gợi ý để HS chứng minh DADE = DEFC. HS: Chứng minh DADE = DEFC theo trường hợp g. c .g GV: Rút ra nhận xét gì từ bài toán trên? HS: Nêu nhận xét. GV: Nhận xét trên chính là nội dung định lí 1 SGK. HS: Đọc định lí 1 ở SGK GV: Giới thiệu DE là đường trung bình của DABC. Vậy đường trung bình của tam giác là gì ? HS: Nêu đ/n như ở SGK. 2.Hoạt động 2: Tìm hiểu tính chất GV: Yêu cầu HS thực hiện theo nhóm ?2 HS: Thực hiện và rút ra kết luận. GV: Dự đoán điều gì từ ?2 HS: GV: Hướng dẫn HS chứng minh bài toán có GT, KL sau GT DABC, AD = DB, AE = EC KL DE // EC, DE = BC Muốn chứng minh DE // BC ta phảI làm gì ? HS: GV: Hướng dẫn HS vẽ thêm đường phụ để chứng minh bài toán. Tứ giác BDFC là hình gì ? Vì sao? HS: BDFC là hình thang vì DB = CF và DB // CF GV: Từ hình thang DBCF hãy suy ra DE // BC và DE = BC HS: Một HS lên bảng trình bày GV: Rút ra nhận xét gì từ bài toán trên ? GV: Giới thiệu định lí 2 cho HS. HS: Đọc nội dung định lí 2 ở SGK 15' 15' 1. Đường trung bình của tam giác GT DABC, AD = DB, DE // BC KL AE = EC Chứng minh: Qua E kẻ đường thẳng song song với AB cắt BC ở F Hình thang DEFB có hai cạnh bên DB // EF nên DB = EF mà DB = AD (gt) AD = EF Xét DADE và DEFC có: A = E1( đồng vị, EF // AB) AD = EF ( cm trên) D1 = F1(= B ) DADE = DEFC(g - c -g) AE = EF . Vậy E là trung điểm của AC. Định lí: SGK Định nghĩa: SGK ?2 GT DABC, AD = DB, AE = EC KL DE // EC, DE = BC Chứng minh: Trên tia đối của ED vẽ điểm F sao cho DE = EF Ta có DAED = DCEF(g - c -g) AD = CE và A = C1 Ta có AD = DB (gt) và AD = CF nên DB = CF. và A = C1 => AD // CF ( vì có cặp góc so le trong bằng nhau) tức là DB // CF Do đó DBCF là hình thang. Hình thang DBCF có hai đáy DB = CF nên hai cạnh bên DF // BC và DF = BC . Do đó: DE // BC DE = DF = BC. Định lí 2:SGK 4. Củng cố- Dặn dò +Củng cố: (5ph) GV: Tính độ dài đoạn BC trên hình vẽ ở bài toán đặt ra ở đầu bài ? HS: Ta có DB = DA, EC = EA nên DE là đường trung bình của DABC Do đó DE = BC => BC = 2DE = 2.50 = 100m. - Nêu định nghĩa về đường trung bình của hình thang, nội dung định lí1, định lí2 + Nhiệm vụ về nhà: (2ph) Học bài theo SGK. Làm các bài tập 20;21;22/SGK Chuẩn bị “ Đường trung bình của hình thang” Ngày soạn: 03/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 6: ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC, CỦA HÌNH THANG (TT) I. MỤC TIÊU 1.Kiến thức - Nắm được định nghĩa, định lí 3, định lí 4 về đường trung bình của hình thang. 2.Kỹ năng: - Biết vận dụng các định lí về đường trung bình của hình thang để tính độ dài, chứng minh hai đoạn thẳng bằng nhau, hai đường thảng song song. - Rèn luyện cách lập luận trong chứng minh định lí và vận dụng các định lí đã học vào các bài toán thực tế. 3.Thái độ: - Rèn đức tính cẩn thận, chính xác trong lập luận chứng minh. II. CHUẨN BỊ 1. Chuẩn bị của gv: Bảng phụ, bút dạ, thước đo góc,compa 2. Chuẩn bị của hs: Học sinh: Bút dạ, thước thẳng, xem lại bài cũ. III.TIẾN TRÌNH BÀI DẠY 1.Ổn định: (1ph) 2 .Kiểm tra bài cũ: (7ph) HS1: Phát biểu định nghĩa và các định lí về đường trung bình của tam giác HS2: Làm bài tập sau: Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F, có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC? 3. Bài mới 1) Đặt vấn đề vào bài(1ph) -Đường trung bình của tam giác thì có tính chất như vậy. Vậy đường trung bình của hình thang thì như thế nào? Đó là nội dung bài học hôm nay. 2) Thiết kế các hoạt động dạy và học Các hoạt động của thày và trò TG Nội dung * Hoạt động 1: Tìm hiểu định lí 3. GV: Qua nội dung bài cũ, vậy đường thẳng đi qua trung điểm một cạnh bên và song song với hai đáy thì như thế nào với cạnh bên thứ 2 ? HS: Đọc định lý trong Sgk. GV: Vẽ hình. HS: Ghi GT và KL. GV: Muốn chứng minh định lí trên ta làm thế nào? HS: Ta dựa vào định lí về đường trung bình của tam giác. GV: Vậy ta cần vẽ thêm đường phụ nào? HS: Kẻ đường cheo AC. GV: Yêu cầu HS lên bảng trình bày chứng minh. HS: Lên bảng trình bày, dưới lớp quan sát và nhận xét. GV: Nhận xét và chốt lại định lí. GV: Ta gọi EF là đường trung bình của hình thang vậy đường trung bình của hình thang là đường như thế nào? HS: Đọc định nghĩa trong Sgk. * Hoạt động 2: Tìm hiểu định lí 4. GV: Gọi HS đọc định lí Sgk. HS: Đọc định lí và cho biết gt và kl. GV: Muốn chứng minh EF // AB (CD) ta dựa vào đâu? HS: Dựa vào tính chất đường trung bình của tam giác. GV:Vậy ta cần vẽ thêm đường phụ nào? HS: Kéo dài AF cắt CD tại K. GV: Yêu cầu HS lên bảng thực hiện. HS: Lên bảng thực hiện. GV: Nhận xét và chốt lại định lí. GV: Yêu cầu HS làm ?5 Sgk. Tính x trên hình vẽ bên HS: Lên bảng thực hiện. 16’ 16’ 2. Đường trung bình của hình thang. Định lí 3. (Sgk) Chứng minh: Gọi I là giao điểm của AC và EF. Tam giác ADC có E là trung điểm của AD và EI //DC => I là trung điểm của AC . Tương tự IF là đường trung bình của tam giác ABC => F là trung điểm của BC . Vậy BF = FC. * Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. * Định lí 4. (Sgk) Chứng minh: Gọi K là giao của AF và CD. Ta có : DABF = DKCB (g.c.g) => AF = FK. và AB = CK. => EF là đường trung bình của tam giác ADK => EF //= DK. hay EF // DC và EF = DC. ?5 Ta có: BE = Hay 32 = => x = 64 - 24 = 40(cm) 4. Củng cố- Dặn dò + Củng cố : (2ph) - Nhắc lại định nghĩa về đường trung bình của hình thang. - Nhắc lại định lí về đường trung bình của hình thang. + Nhiệm vụ về nhà: (2ph) - Học thuộc định nghĩa, định lí về đường trung bình của hình thang. - Làm bài tập 23, 25, 25, 27 SGK. Ngày soạn: 16/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 7: LUYỆN TẬP I. MỤC TIÊU 1.Kiến thức : - Củng cố và nắm chắc các định lí, định nghĩa và tính chất đường trung bình của tam giác và hình thang. 2.Kỹ năng: - Biết vận dụng các định lí về đường trung bình của tam giác và hình thang để tính độ dài, chứng minh hai đoạn thẳng bằng nhau, hai đường thẳng song song. - Rèn luyện cách lập luận trong chứng minh và vận dụng các định lí đã học vào các bài toán thực tế. 3.Thái độ: - Rèn đức tính cẩn thận, chính xác trong tính toán và lập luận chứng minh. II. CHUẨN BỊ Chuẩn bị của gv: Bảng phụ, bút dạ, thước đo góc. Chuẩn bị của hs: Bút dạ, thước thẳng, xem lại bài cũ. III.TIẾN TRÌNH LÊN LỚP 1. Ổn định: (1ph) 2. Kiểm tra bài cũ: (10ph) HS1: Phát biểu định nghĩa và các định lí về đường trung bình hình thang. HS2: Chữa bài tập 26. GV: Nhận xét và chốt lại nội dung đường trung bình của hình thang. 3 Bài mới: 1) Đặt vấn đề. (1ph) Chúng ta đã nắm được định nghĩa đường trung bình của tam giác và hình thang cũng như các tính chất của nó hôm nay thầy trò ta cùng đi giải một số bài tập liên quan đến đường trung bình của hình thang và tam giác. 2) Thiết kế các hoạt động dạy và học Ho¹t ®éng cña GV và HS TG Néi dung kiÕn thøc * Hoạt động 1: Bài tập 27. GV: Gọi HS đọc đề bài tập và lên bảng vẽ hình. HS: Làm theo yêu cầu của GV GV: Yêu cầu HS cho biết giả thiết và kết luận. GV: Muốn so sánh EK và CD, KF và AB ta làm thế nào? HS: Dựa và tính chất đường phân giác của tam giác. GV: Yêu cầu HS lên bảng thực hiện. HS: lên bảng thực hiện, dưới lớp làm vào nháp. GV: Cùng HS nhận xét kết quả. GV: Muốn chứng minh EF < . ta dựa vào đâu? HS: Dựa vào câu a và tính chất tổng hai cạnh trong tam giác thì lớn hơn cạnh thức ba. GV: Yêu cầu HS lên bảng giải. HS: Lên bảng thực hiện. GV: Từ bài tập đó em nào có thể nêu lân bài toán tổng quát về tính chất trên? HS: " EF là độ dài đoạn thẳng nối trung điểm hai cạnh đối AD và BC của tứ giác ABCD. Chứng minh rằng: EF < . Dấu bằng sảy ra khi ABCD là hình thang. * Hoạt động 2: Bài tập 28 GV: Yêu cầu HS đọc đề bài toán. HS: Vẽ hình ghi GT và KL GV: Để chứng minh I là trung điểm của BD và K là trung điểm của AC ta làm thế nào? HS: Dựa vào đường trung bình của tam giác. GV: Yêu cầu HS lên bảng thực hiện. HS: Lên bảng trình bày. GV: Nhận xét và chốt lại. 15’ 14’ 1. Bài tập 27. a) Ta có: E là trung điểm của AD. K là trung điểm của AC. Nên EK là đường trung bình của tam giác ADC. => EK = DC. Tương tự ta có: FK = AB. b) Ta thấy. EF < EK + FK => EF < . 2. Bài tập 28. Giải. a) Ta có: EF là đường trung bình của hình thang => EF // AB và EF // CD. Xét DADC có E là trung điểm của AD và EK // DC => K là trung điểm của AC hay AK = KC. Tương tự: Xét DADB có E là trung điểm của AD và EI // AB => I là trung điểm của AB hay BI = ID. b) Ta có: EF = (AB + DC) = (6 + 10) = 8 cm. EI = 6:2 = 3 cm. KF = 6:2 = 3 cm IK = 8 - (3 + 3) = 2 cm 4. Củng cố- Dặn dò + Củng cố: (2ph) - Nhắc lại định nghĩa, định lí về đường trung bình của tam giác và hình thang. +Nhiệm vụ về nhà : (2ph) - Học thuộc định nghĩa, định lí về đường trung bình của tam giác và hình thang. - Làm bài tập 29, 30, 31 SGK Ngày soạn: 16/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 8: ĐỐI XỨNG TRỤC I. MỤC TIÊU 1.Kiến thức: - Giúp HS củng cố vững chắc định nghĩa hai điểm đối xứng nhau qua 1 trục; hai đoạn thẳng, hai hình đối xứng nhau qua đường thẳng - Biết dựng một điểm đối xứng ,một đoạn đối xứng cho trước. 2.Kỹ năng: - Giúp Hs chứng minh được một điểm đối xứng với một điểm,một đoạn thẳng đối xứng với một đoạn thẳng qua một trục. 3.Thái độ: - Rèn khả năng vận dụng nhanh nhẹn, hoạt bát. Biết vận dụng. II. CHUẨN BỊ Chuẩn bị của gv: Bảng phụ, bút dạ, thước, compa, êke Chuẩn bị của hs: Bút dạ, thước thẳng, com pa, êke. III. TIẾN TRÌNH BÀI DẠY 1. Ổn định (1ph) 2. Kiểm tra bài cũ (5ph) Nêu định nghĩa đường trung trực của đoạn thẳng 3. Bài mới 1) Đặt vấn đề vào bài. (5ph) - Giáo viên dùng một tờ giấy gấp 4 lại và cắt thành chữ cái H in hoa.Vậy vì sao ta có thể gấp tờ giấy thành tư để cắt thành chữ H. Bài học hôm nay sẽ giúp ta giải quyết điều này. 2) Thiết kế các hoạt động dạy và học Ho¹t ®éng cña GV và HS TG Néi dung *Hoạt động 1: Tìm hiểu hai điểm đối xứng nhau qua một dường thẳng GV: Quay lại phần kiểm tra bài cũ để giới thiệu hai điểm đối xứng nhau qua một đường thẳng. HS: Nhắc lại định nghĩa trong Sgk. GV: Nếu điểm M nằm trên trục đối xứng d thì điểm đối xứng với điểm M là điểm nào? HS: Điểm đối xứng với điểm M cũng là M. *Hoạt động 2: Tìm hiểu hai hình đối xứng nhau qua một dường thẳng GV: Cho HS hoạt động theo nhóm làm bài tập sau: Cho đường thẳng d và doạn thẳng AB. - Vẽ điểm A' đối xứng với A qua d - Vẽ điểm B' đối xứng với B qua d - Lấy điểm C thuộc đoạn thẳng AB, vẽ diểm C' đối xứng với C qua d. - Dùng thước để kiểm nghiệm rằng điểm C' thuộc đoạn thẳng A'B'. HS: Làm trên giấy nháp. Nhận xét: Nếu A, B, C thẳng hàng thì điểm đối xứng với nó qua 1 đường thẳng cũng thẳng hàng. GV: Thu phiếu và cho các nhóm tự nhận xét két quả của nhau. -Vậy hai hình đối xứng nhau qua đường thẳng d khi nào? HS: Phát biểu định nghĩa. *Hoạt động 3: Hình có trục đối xứng Cho tam giác ABC cân tại A, đường cao AH. Tìm hình đối xứng với mỗi cạnh của tam giác ABC qua AH. GV: Gọi HS vẽ hình và nêu nhận xét HS:- A đối xứng với chính nó qua AH - B đối xứng với chính nó qua AH - H đối xứng với chính nó qua AH *Kết luận: Mọi điểm của tam giác ABC đối xứng qua AH đều thuộc tam giác ABC. GV: Giới thiêụ hình có trục đối xứng HS: Đọc định nghĩa trong Sgk. GV: Yêu cầu HS làm [?4] trong Sgk. Mỗi hình sau có bao nhiêu trục đối xứng. a) Chữ cái in hoa A. b) Tam giác đều ABC. c) Đường tròn tâm O. HS: Thảo luận rồi trả lời. GV: Dùng giấy đề can vẽ một hình thang cân, gấp hình và thử phát hiện hình thang cân có phải là hình có trục đối xứng không? HS: Nhận xét . 10' 10' 10' 1.Hai điểm đối xứng nhau qua một đường thẳng. A . . B (d) * Định nghĩa: (Sgk) *Chú ý: Điểm MÎd thì điểm đối xứng với M qua d cũng là điểm M. 2.Hai hình đối xứng nhau qua một đường thẳng. A (d) A' C' B' C B * Định nghĩa: (Sgk) * Nhận xét: Hai tam giác,hai góc, hai hình đối xứng nhau qua một đường thẳng thì bằng nhau. 3.Hình có trục đối xứng. * Định nghĩa: (Sgk) ?4 A O C B a) Chữ cái in hoa A có một trục đối xứng. b) Tam giác đều ABC có ba trục đối xứng. c) Đường tròn tâm O có vô số trục đối xứng. K H D C B A Đường thẳng đi qua trung điểm của hai đáy hình thang cân là trục đối xứng của hình thang cân đó. 4. Củng cố- Dặn dò + Củng cố: (3ph) - Nhắc lại định nghĩa, định lí về đường trung bình của tam giác và hình thang. + Nhiệm vụ về nhà: (1ph) - Học thuộc định nghĩa, định lí về đường trung bình của tam giác và hình thang Ngày soạn: 16/09/2017 Ngày dạy: +Lớp 8A: /09/2017 +Lớp 8C: /09/2017 Tiết 9: LUYỆN TẬP I. MỤC TIÊU 1.Kiến thức : - Giúp học sinh có điều kiện nắm chắc hơn khái niệm đối xứng trục ,hình có trục đối xứng. Tính chất của hai đoạn thẳng, hai tam giác, hai góc đối xứng nhau. 2.Kỹ năng: - Rèn kỹ năng phân tích, tổng hợp qua việc tìm tòi lời giải cho một bài toán. 3.Thái độ: - Rèn khả năng vận dụng nhanh nhẹn,hoạt bát. II. CHUẨN BỊ Chuẩn bị của gv: Bảng phụ, bút dạ, thước . Chuẩn bị của hs: Bút dạ, thước thẳng, làm bài tập về nhà. III.TIẾN TRÌNH BÀI DẠY 1.Ổn định: (1ph) 2.Kiểm tra bài cũ (5ph) - Phát biểu các định nghĩa. Hai điểm đối xứng nhau qua một đường thẳng, hai hình đối xứng nhau qua một đường thẳng, hình có trục đối xứng. 3. Bài mới 1) Đặt vấn đề vào bài. - Để khắc sâu kiến thức về các khai niệm đó. Hôm nay cô trò ta cùng làm một số bài tập về phần này. 2) Thiết kế các hoạt động dạy và học Các hoạt động của thày và trò TG Nội dung 1. Cho góc xOy có số đo 500 , điểm A nằm trong góc đó, vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. a) So sánh OB và OC. b) Tính số đo góc BOC. GV: Yêu cầu học sinh lên bảng vẽ hình. HS: 1 em lên bảng vẽ, dưới lớp làm vào vở. GV: Qua hình bạn vẽ trên bảng em nào cho thầy biết muốn so sánh OB và OC ta làm thế nào? HS: Xung phong lên bảng trình bày, dưới lớp làm vào vở. GC:Nhận xét và sửa sai. 2.Cho hai điểm A, B thuộc cùng một nữa mặt phẳng có bờ là đường thẳng d. Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn BC. Gọi E là điểm bất kì của đường thẳng d (E khác D). Chứng minh rằng AD+DB < AE+EB. GV: Đưa đề và hình lên bảng phụ HS: Quan sát và tiến hành làm, 1 em lên bảng thực hiện, dưới lớp là vào nháp. GV: Hỏi thêm. Nếu bạn Tú đang ở vị trí A, cần đến bờ sông d lấy nước rồi đi đến vị trí B. Vậy con đường ngắn nhất bạn tú nên đi là con đường nào? HS: Con đường ngắn nhất
Tài liệu đính kèm:
 giao_an_hinh_hoc_lop_8_chuong_1_tu_giac_vi_van_yen.doc
giao_an_hinh_hoc_lop_8_chuong_1_tu_giac_vi_van_yen.doc



