Các chuyên đề ôn thi học sinh giỏi môn Toán Lớp 8 - Chuyên đề 9: Các bài toán sử dụng định lí Talét và tính chất đường phân giác

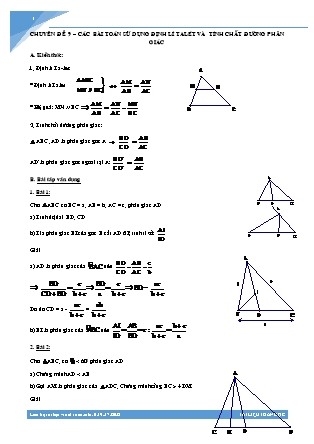
CHUYÊN ĐỀ 9 – CÁC BÀI TOÁN SỬ DỤNG ĐỊNH LÍ TALÉT VÀ TÍNH CHẤT ĐƯỜNG PHÂN GIÁC
A. Kiến thức:
1. Định lí Ta-lét:
* Định lí Talét 
* Hệ quả: MN // BC 
2. Tính chất đường phân giác: 
ABC ,AD là phân giác góc A 
AD’là phân giác góc ngoài tại A: 
B. Bài tập vận dụng
1. Bài 1:
Cho ABC có BC = a, AB = b, AC = c, phân giác AD
a) Tính độ dài BD, CD
b) Tia phân giác BI của góc B cắt AD ở I; tính tỉ số: 
Giải
a) AD là phân giác của nên 
Do đó CD = a - = 
b) BI là phân giác của nên 
2. Bài 2:
Cho ABC, có < 600 phân giác AD
a) Chứng minh AD < AB
b) Gọi AM là phân giác của ADC. Chứng minh rằng BC > 4 DM
Giải
a)Ta có > = 
 > AD < AB
 b) Gọi BC = a, AC = b, AB = c, AD = d
Trong ADC, AM là phân giác ta có
 DM = ; CD = ( Vận dụng bài 1) DM = 
Để c/m BC > 4 DM ta c/m a > hay (b + d)(b + c) > 4bd (1)
Thật vậy : do c > d (b + d)(b + c) > (b + d)2 4bd . Bất đẳng thức (1) được c/m
3.Bài 3:
Cho ABC, trung tuyến AM, các tia phân giác của các góc AMB , AMC cắt AB, AC theo thứ tự ở D và E
a) Chứng minh DE // BC
b) Cho BC = a, AM = m. Tính độ dài DE
c) Tìm tập hợp các giao diểm I của AM và DE nếu ABC có BC cố định, AM = m không đổi
d) ABC có điều kiện gì thì DE là đường trung bình của nó
Giải
a) MD là phân giác của nên (1)
 ME là phân giác của nên (2)
Từ (1), (2) và giả thiết MB = MC ta suy ra DE // BC
b) DE // BC . Đặt DE = x 
c) Ta có: MI = DE = không đổi I luôn cách M một đoạn không đổi nên tập hợp các điểm I là đường tròn tâm M, bán kính MI = (Trừ giao điểm của nó với BC
d) DE là đường trung bình của ABC DA = DB MA = MB ABC vuông ở A
4. Bài 4: 
Cho ABC ( AB < AC) các phân giác BD, CE
a) Đường thẳng qua D và song song với BC cắt AB ở K, chứng minh E nằm giữa B và K
b) Chứng minh: CD > DE > BE
Giải
a) BD là phân giác nên 
 (1)
Mặt khác KD // BC nên (2)
Từ (1) và (2) suy ra 
 E nằm giữa K và B
b) Gọi M là giao điểm của DE và CB. Ta có (so le trong)
 mà E nằm giữa K và B nên > > > EB < DE
Ta lại có > > (Vì = )
Suy ra: CD > ED CD > ED > BE
5. Bài 5: Cho ABC . Ba đường phân giác AD, BE, CF. Chứng minh
a. .
b. . 
Giải
a)AD là đường phân giác của nên ta có: (1)
Tương tự: với các phân giác BE, CF ta có: (2) ; (3)
Từ (1); (2); (3) suy ra: = 1
b) §Ỉt AB = c , AC = b , BC = a , AD = da. 
Qua C kỴ ®­êng th¼ng song song víi AD , c¾t tia BA ë H. 
Theo §L TalÐt ta cã: 
Do CH < AC + AH = 2b nªn: 
Chøng minh t­¬ng tù ta cã : Vµ Nªn: 
 ( ®pcm )
Bµi tËp vỊ nhµ
Cho ABC có BC = a, AC = b, AB = c (b > c), các phân giác BD, CE
a) Tính độ dài CD, BE rồi suy ra CD > BE
b) Vẽ hình bình hành BEKD. Chứng minh: CE > EK
c) Chứng minh CE > BD