Giáo án Hình học Lớp 8 - Bài 1: Tứ giác
A. KIẾN THỨC TRỌNG TÂM
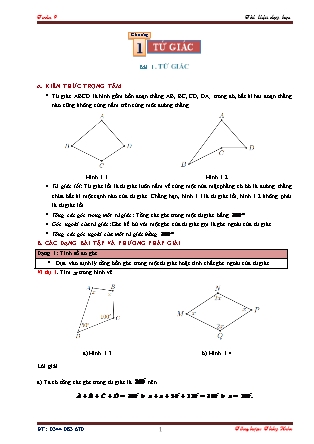
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA; trong đó, bất kì hai đoạn thẳng nào cũng không cùng nằm trên cùng môt đường thẳng.
Hình 1.1 Hình 1.2
Tứ giác lồi: Tứ giác lồi là tứ giác luôn nằm về cùng một nửa mặt phẳng có bờ là đường thẳng chứa bất kì một cạnh nào của tứ giác. Chẳng hạn, hình 1.1 là tứ giác lồi; hình 1.2 không phải là tứ giác lồi.
Tổng các góc trong một tứ giác: Tổng các góc trong một tứ giác bằng .
Góc ngoài của tứ giác: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
Tổng các góc ngoài của một tứ giác bằng .
Bạn đang xem tài liệu "Giáo án Hình học Lớp 8 - Bài 1: Tứ giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chương 1 TỨ GIÁC Bài 1. TỨ GIÁC A. KIẾN THỨC TRỌNG TÂM Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA; trong đó, bất kì hai đoạn thẳng nào cũng không cùng nằm trên cùng môt đường thẳng. Hình 1.1 Hình 1.2 Tứ giác lồi: Tứ giác lồi là tứ giác luôn nằm về cùng một nửa mặt phẳng có bờ là đường thẳng chứa bất kì một cạnh nào của tứ giác. Chẳng hạn, hình 1.1 là tứ giác lồi; hình 1.2 không phải là tứ giác lồi. Tổng các góc trong một tứ giác: Tổng các góc trong một tứ giác bằng . Góc ngoài của tứ giác: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác. Tổng các góc ngoài của một tứ giác bằng . B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI Dạng 1: Tính số đo góc Dựa vào định lý tổng bốn góc trong một tứ giác hoặc tính chất góc ngoài của tứ giác. Ví dụ 1. Tìm trong hình vẽ. a) Hình 1.3 b) Hình 1.4 Lời giải a) Ta có tổng các góc trong tứ giác là nên b) Ta có tổng các góc trong tứ giác là nên . Ví dụ 2. Tứ giác có , , . Tính số đo góc ngoài tại đỉnh . Lời giải Xét tứ giác , ta có Khi đó, góc ngoài tại đỉnh có số đo . Dạng 2: Chứng minh hình học Vận dụng các kiến thức đã học ở lớp 7 về tam giác, chu vi, đường trung trực của đoạn thẳng; các đường đặc biệt trong tam giác, để chứng minh. Ví dụ 3. Cho tứ giác , là giao điểm của hai đường chéo và . Chứng minh: a) ; b) . Lời giải a) Áp dụng bất đẳng thức trong tam giác ta có . b) Tương tự trên, áp dụng bất đẳng thức trong tam giác ta có và C. BÀI TẬP VẬN DỤNG Bài 1. Cho tứ giác có ; . a) Chứng minh là đường trung trực của ; b) Cho , . Tính và . Lời giải a) Vì suy ra thuộc đường trung trực của . Vì thuộc đường trung trực của . là đường trung trực của . b) Xét và có (giả thiết); (giả thiết); : cạnh chung. (c.c.c), suy ra . Vậy . Bài 2. Cho tứ giác , biết rằng . Tính các góc của tứ giác . ĐS: , ; , . Lời giải Áp dụng tính chất dãy tỉ số bằng nhau Vậy , ; , . Bài 3. Cho tứ giác có , , . Hãy tính các góc của tứ giác . ĐS: ; ; ; . Lời giải Ta có . Thay , , vào biểu thức trên, ta được . Vậy ; ; ; . Bài 4. Tứ giác có , , . Tính số đo của và . ĐS: , . Lời giải Ta có mà . , . Bài 5. Cho tứ giác có hai đường chéo và vuông góc với nhau tại . a) Chứng minh ; b) Cho cm, cm, cm. Tính độ dài . ĐS: cm. Lời giải a) Áp dụng định lý Pytago vào các tam giác vuông , ta có . Áp dụng định lý Pytago vào các tam giác vuông , ta có . Áp dụng định lý Pytago vào các tam giác vuông , ta có . Áp dụng định lý Pytago vào các tam giác vuông , ta được b) Theo câu trên, ta có D. BÀI TẬP VỀ NHÀ Bài 6. Tìm trong hình vẽ. a) Hình 1.5 b) Hình 1.6 c) Hình 1.7 d) Hình 1.8 ĐS: a) ; b) ; c) ; d) . Lời giải a) Ta có tổng các góc trong tứ giác là nên b) Ta có tổng các góc trong tứ giác là nên c) Ta có tổng các góc trong tứ giác là nên d) Vì góc ngoài tại có số đo là nên . Góc ngoài tại có số đo là nên . Ta có tổng các góc trong tứ giác là nên . Bài 7. Cho tứ giác biết , , . Tính số đo các góc ngoài của tứ giác . Lời giải Xét tứ giác , ta có Khi đó, ta có Góc ngoài tại có số đo là . Góc ngoài tại có số đo là . Góc ngoài tại có số đo là . Góc ngoài tại có số đo là . Bài 8. Cho tứ giác . Gọi là giao điểm của hai đường chéo và . Gọi chu vi của tứ giác là . Chứng minh: a) ; b) Nếu thì . Lời giải a) Theo kết quả bài trên, ta có Cộng vế với vế . b) Áp dụng bất đẳng thức tam giác vào các tam giác , : ; . Tương tự . --- HẾT ---
Tài liệu đính kèm:
 giao_an_hinh_hoc_lop_8_bai_1_tu_giac.docx
giao_an_hinh_hoc_lop_8_bai_1_tu_giac.docx



