Giáo án Hình học Lớp 8 - Bài 4: Đường trung bình của tam giác

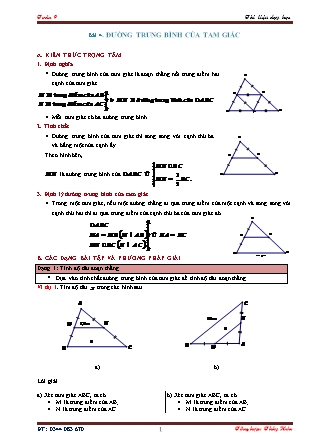
Bài 4. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
A. KIẾN THỨC TRỌNG TÂM
1. Định nghĩa
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
.
Mỗi tam giác có ba đường trung bình.
2. Tính chất
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một nửa cạnh ấy.
Theo hình bên,
 là đường trung bình của 
3. Định lý đường trung bình của tam giác
Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba của tam giác đó.
.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính độ dài đoạn thẳng
Dựa vào tính chất đường trung bình của tam giác để tính độ dài đoạn thẳng.
Ví dụ 1. Tìm độ dài trong các hình sau
	a)	b)
Lời giải
a) Xét tam giác ABC, ta có
M là trung điểm của AB;
N là trung điểm của AC.
 là đường trung bình của .
.
b) Xét tam giác ABC, ta có
M là trung điểm của AB;
N là trung điểm của AC.
 là đường trung bình của .
.
Ví dụ 2. Cho tam giác vuông tại , , . Qua trung điểm của , vẽ một đường thẳng song song với cắt tại . Tính độ dài .
Lời giải
Xét có và nên . Do đó, là đường trung bình. Suy ra .
Vì vuông tại nên 
 .
Vậy .
Dạng 2: Chứng minh hai đoạn thẳng bằng nhau; hai đường thẳng song song.
Sử dụng tính chất đường trung bình của tam giác.
Sử dụng dấu hiệu nhận biết hai đường thẳng song song, hai đoạn thẳng bằng nhau như đã học ở lớp 7.
Ví dụ 3. Cho tam giác , các đường trung tuyến , . Gọi , theo thứ tự là trung điểm của và . Gọi , theo thứ tự là giao điểm của với và . Chứng minh .
Lời giải
Xét có .
Xét có .
Suy ra ; ; .
.
Vậy .
Ví dụ 4. Cho tam giác , điểm , thuộc sao cho . Gọi là trung điểm của , là giao điểm của và . Chứng minh
a) ;	b) .
Lời giải
a) Xét có .
b) Xét có .
Dạng 3: Sử dụng tính chất đường trung bình của tam giác để chứng minh yếu tố hình học
Vận dụng định nghĩa, tính chất và định lý đường trung bình của tam giác để chứng minh.
Ví dụ 5. Cho tam giác , các đường trung tuyến , cắt nhau tại . Gọi , lần lượt là trung điểm , . Chứng minh tứ giác có các cặp cạnh đối song song và bằng nhau.
Lời giải
 Xét có 
 Xét có 
 Từ và .
 Xét có 
 Xét có 
 Từ và .
 Vậy tứ giác có các cặp cạnh đối song song và bằng nhau.
Ví dụ 6. Cho là đường trung tuyến của tam giác , là trung điểm của đoạn thẳng , là trung điểm đoạn thẳng , là trung điểm cạnh , là trung điểm cạnh . Chứng minh và .
Lời giải
Xét có .
Xét có .
Từ và 
C. BÀI TẬP VẬN DỤNG
Bài 1. Cho tam giác , là trung điểm , là một điểm nằm trên cạnh sao cho . Gọi là giao điểm của và . Chứng minh là trung điểm của .
Lời giải
Gọi là trung điểm và là trung điểm .
 là đường trung bình của là trung điểm của .
Bài 2. Cho tam giác , trung tuyến . Gọi là trung điểm , là giao điểm của và .
a) Chứng minh ;	b) So sánh độ dài và .
Lời giải
a) Kẻ , .
 là đường trung bình trong 
 là trung điểm của .
 là đường trung bình trong 
 là trung điểm của .
Từ và suy ra .
Có ; , nên .
Bài 3: Cho tam giác , đường trung tuyến . Gọi là một điểm trên cạnh sao cho . Gọi là giao điểm của và . Chứng minh rằng
a) là trung điểm của .	b) .
Lời giải
a) Qua vẽ một đường thẳng song song với cắt tại .
Xét có và nên
 (định lý đường trung bình của tam giác).
Mặt khác , do đó .
Xét có và nên hay O là trung điểm của AD.
b) Xét có là đường trung bình nên .	(1)
Xét có là đường trung bình nên .	(2)
Từ (1) và (2) suy ra .
D. BÀI TẬP VỀ NHÀ
Bài 4. Cho tam giác , hai đường trung tuyến và cắt nhau tại . Gọi và lần lượt là trung điểm của và . Chứng minh rằng
a) . 	b) .
Lời giải
a) Vì , là các đường trung tuyến của nên , .
Do đó là đường trung bình của , suy ra . 	(1)
Ta có là đường trung bình của nên . 	(2)
Từ (1) và (2) suy ra .
b) Xét , ta có là đường trung bình.
Xét , ta có là đường trung bình. Do đó , . Suy ra .
Bài 5. Cho tam giác , đường trung tuyến . Gọi , , lần lượt là trung điểm của , và . Chứng minh rằng
a) Ba điểm , , thẳng hàng.	b) là trung điểm của .
Lời giải
a) Xét có là đường trung bình nên hay . 	(1)
Xét có là đường trung bình nên , 	(2)
Từ (1) và (2) suy ra , , thẳng hàng.
b) Chứng minh (bằng của hai đoạn thẳng bằng nhau).
Bài 6. Cho tam giác vuông tại , đường cao . Gọi và lần lượt là trung điểm của và . Chứng minh rằng .
Lời giải
Xét có là đường trung bình nên .
Xét có và là hai đường cao cắt nhau tại .
Do đó 
--- HẾT ---