Giáo án Hình học Lớp 8 - Bài: Ôn tập chương I

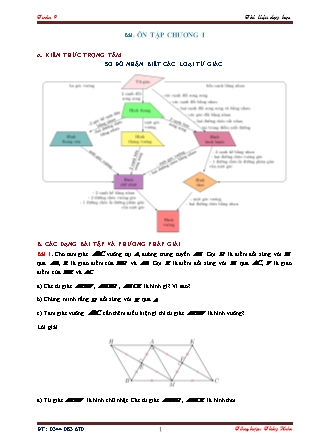
Bài. ÔN TẬP CHƯƠNG I
A. KIẾN THỨC TRỌNG TÂM
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Bài 1. Cho tam giác vuông tại , đường trung tuyến . Gọi là điểm đối xứng với qua , là giao điểm của và . Gọi là điểm đối xứng với qua , là giao điểm của và .
a) Các tứ giác , , là hình gì? Vì sao?
b) Chứng minh rằng đối xứng với qua .
c) Tam giác vuông cần thêm điều kiện gì thì tứ giác là hình vuông?
Lời giải
a) Tứ giác là hình chữ nhật. Các tứ giác , là hình thoi.
b) Theo a) suy ra , , , thẳng hàng. Lại có , đối xứng với nhau qua .
c) Để hình chữ nhật là hình vuông thì cần thêm điều kiện . . Vậy tam giác vuông cân tại .
Bài 2. Cho hình bình hành có , . Gọi , theo thứ tự là trung điểm của , . Vẽ đối xứng với qua .
a) Tứ giác là hình gì? Vì sao?
b) Chứng minh tứ giác là hình thang cân.
c) Chứng minh là hình chữ nhật.
d) Tính góc .
Lời giải
a) Vì Tứ giác là hình thoi.
b) Dễ thấy , ; đều. Do đó, suy ra là hình thang cân.
c) là hình thoi. Suy ra là đường phân giác trong của .
Có và hay . Vậy tứ giác là hình bình hành vì có cặp cạnh đối song song và bằng nhau.
Thấy rằng vừa là đường trung tuyến, phân giác của . Suy ra hay Tứ giác là hình chữ nhật vì là hình bình hành có một góc vuông.
d) Vì là hình chữ nhật nên là trung điểm của . Ta có cân tại , mà là đường trung tuyến nên đồng thời là đường cao. Suy ra , vậy .
Bài 3. Cho hình thang cân , các đường cao , .
a) Tứ giác là hình gì? Vì sao?
b) Chứng minh .
c) Gọi là điểm đối xứng với qua . Các điểm và đối xứng với nhau qua đường nào?
d) Tứ giác là hình gì?
Lời giải
a) Tứ giác là hình chữ nhật.
b) (ch - gn). 
Nên suy ra .
c) và đối xứng với nhau qua đường thẳng .
d) Dễ thấy . Do đó, là hình bình hành.
Bài 4. Cho tam giác vuông tại . Gọi lần lượt là trung điểm của , . Kẻ song song với cắt tại .
a) Chứng minh tứ giác là hình chữ nhật.
b) Gọi đối xứng với qua . Tứ giác là hình gì? Vì sao?
c) Gọi đối xứng với qua . Tứ giác là hình gì? Vì sao?
d) Tam giác cần thêm điều kiện gì để tứ giác là hình vuông?
Lời giải
a) Tứ giác là hình chữ nhật vì có 3 góc vuông.
 là đường trung bình của tam giác .
 là hình chữ nhật.
b) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường. Lại có nên là hình chữ nhật.
c) Tứ giác là hình thoi vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và (trung tuyến ứng với cạnh huyền).
d) Tam giác vuông cân.
C. BÀI TẬP VẬN DỤNG
Bài 1. Cho tam giác vuông tại có . Gọi là trung điểm của , kẻ vuông góc với tại , vuông góc với tại .
a) Chứng minh .
b) Chứng minh tức giác là hình bình hành.
c) Gọi là đường cao của tam giác (). Chứng minh tứ giác là hình thang cân và đối xứng với qua .
Lời giải
a) Dễ thấy là hình chữ nhật, suy ra đpcm.
b) Dễ thấy , đpcm.
c) ; nên là hình thang cân và , đối xứng với nhau qua .
Bài 2. Cho hình thang vuông có và , kẻ vuông góc với .
a) Chứng minh rằng tứ giác là hình vuông.
b) Gọi là trung điểm của . Chứng minh đối xứng với qua .
c) Kẻ vuông góc với . cắt , tại và . Chứng minh tứ giác là hình thoi.
Lời giải
a) là hình vuông vì là hình chữ nhật và có hai cạnh kề bằng nhau.
b) Có và nên tứ giác là hình bình hành. là trung điểm của . Vậy đối xứng với qua .
c) Có (c.g.c) nên ; (c.g.c) nên .
Lại có (cùng phụ với góc ) (vì ). Vậy (g.c.g) Tứ giác là hình thoi vì có bốn cạnh bằng nhau.
Bài 3. Cho hình chữ nhật . Gọi là chân đường vuông góc kẻ từ đến . Gọi , theo thứ tự là trung điểm của các đoạn và .
a) Chứng minh .
b) Gọi là trung điểm của cạnh . Chứng minh tứ giác là hình bình hành.
c) Chứng minh tam giác vuông.
Lời giải
a) là đường trung bình của tam giác .
b) ;
Mà là hình bình hành.
c) Dễ dàng chứng minh là trực tâm của . Vậy vuông tại .
Bài 4. Cho hình vuông . là điểm trên cạnh , là điểm trên tia đối của tia sao cho .
a) Chứng minh tam giác vuông cân.
b) Gọi là trung điểm của . Chứng minh thuộc .
c) Lấy điểm đối xứng với qua . Chứng minh tứ giác là hình vuông.
Lời giải
a) ; . Dễ thấy . Do đó, là tam giác vuông cân tại .
b) Chứng minh . Do đó nằm trên đường trung trực của . Mà là đường trung trực của (tính chất hình vuông ) nên .
c) Vì là tam giác vuông cân nên . Hơn nữa và nên . Vậy tứ giác là hình vuông.
D. BÀI TẬP VỀ NHÀ
Bài 5. Cho tam giác vuông tại , đường trung tuyến . Gọi là trung điểm của , là điểm đối xứng của qua .
a) Chứng minh đối xứng với qua đường thẳng .
b) Các tứ giác , là hình gì? Vì sao?
c) Tam giác vuông cần thêm điều kiện gì thì tứ giác là hình vuông?
Lời giải
a) Vì nên đối xứng với qua đường thẳng .
b) Có và cắt nhau tại trung điểm của mỗi đường nên tứ giác là hình bình hành. . Vậy tứ giác cũng là hình bình hành vì có hay và .
c) Hình bình hành có hai đường chéo vuông góc với nhau nên là hình thoi. Để hình thoi là hình vuông thì cần điều kiện . Vì tứ giác là hình bình hành nên . Vậy nếu suy ra . Lúc này tam giác cân tại . Vậy để tứ giác là hình vuông thì tam giác vuông cần thêm điều kiện hay tam giác vuông cân tại .
Bài 6. Cho hình bình hành có và . Gọi lần lượt là trung điểm của và là điểm đối xứng của qua .
a) Tứ giác là hình gì? Vì sao?
b) Chứng minh tam giác đều.
c) Chứng minh tứ giác là hình chữ nhật.
Lời giải
a) Vì Tứ giác là hình thoi.
b) Tam giác có nên cân tại và nên là tam giác đều.
c) Dễ dàng nhận thấy tứ giác là hình bình hành. Vì tam giác là tam giác đều nên . Vậy tam giác có là đường trung tuyến và nên tam giác là tam giác vuông tại (trong tam giác vuông trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền). Vậy hình bình hành có một góc vuông nên tứ giác là hình chữ nhật.
Bài 7. Cho tứ giác , là trung điểm của cạnh . Qua kẻ đường thẳng song song với cắt ở . Qua kẻ đường thẳng song song với cắt ở . Qua kẻ đường thẳng song song với cắt ở .
a) Chứng minh tứ giác là hình bình hành.
b) Tứ giác cần thêm điều kiện gì để tứ giác là hình chữ nhật.
Lời giải
a) Có và nên tứ giác là hình bình hành vì có các cặp đối song song với nhau.
b) Để tứ giác là hình chữ nhật thì hay vì và . Vậy điều kiện để tứ giác là hình chữ nhật thì tứ giác phải có hai đường chéo vuông góc. 
Bài 8. Cho tam giác vuông ở . Gọi , , lần lượt là trung điểm của , , . Từ kẻ đường thẳng song song với , đường thẳng này cắt tại .
a) Tứ giác là hình gì? Vì sao?
b) Chứng minh tứ giác là hình bình hành.
c) Chứng minh tứ giác là hình thoi.
d) Tìm điều kiện của tam giác để tứ giác là hình vuông.
Lời giải
a) Tứ giác là hình chữ nhật vì có 3 góc vuông. 
b) Có hay . Vậy tứ giác là hình bình hành vì có hai cặp cạnh đối song song.
c) Tứ giác là hình thoi vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và vuông góc với nhau ().
d) Để tứ giác là hình vuông thì . Vậy tam giác sẽ thành tam giác vuông cân tại .
--- HẾT ---