Các chuyên đề ôn thi học sinh giỏi môn Toán Lớp 8 - Chuyên đề 11: Vẽ đường thẳng song song để tạo thành các cặp đoạn thẳng tỷ lệ
CHUYÊN ĐỀ 11 – VẼ ĐƯỜNG THẲNG SONG SONG ĐỂ TẠO THÀNH CÁC CẶP ĐOẠN THẲNG TỶ LỆ
A. Phương pháp:
Trong các bài tập vận dụng định lí Talét. Nhiều khi ta cần vẽ thêm đường phlà một đường thẳng song song với một đường thẳng cho trước,. Đây là một cách vẽ đường phụ hay dùng, vì nhờ đó mà tạo thành được các cặp đoạn thẳng tỉ lệ
B. Các ví dụ:
1) Ví dụ 1:
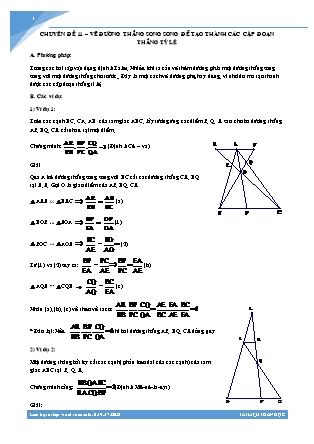
Trên các cạnh BC, CA, AB của tam giác ABC, lấy tương ứng các điểm P, Q, R sao cho ba đường thẳng AP, BQ, CR cắt nhau tại một điểm.
Chứng minh: (Định lí Cê – va)
Giải
Qua A kẻ đường thẳng song song với BC cắt các đường thẳng CR, BQ tại E, F. Gọi O là giao điểm của AP, BQ, CR
Bạn đang xem tài liệu "Các chuyên đề ôn thi học sinh giỏi môn Toán Lớp 8 - Chuyên đề 11: Vẽ đường thẳng song song để tạo thành các cặp đoạn thẳng tỷ lệ", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHUYÊN ĐỀ 11 – VẼ ĐƯỜNG THẲNG SONG SONG ĐỂ TẠO THÀNH CÁC CẶP ĐOẠN THẲNG TỶ LỆ A. Phương pháp: Trong các bài tập vận dụng định lí Talét. Nhiều khi ta cần vẽ thêm đường phlà một đường thẳng song song với một đường thẳng cho trước,. Đây là một cách vẽ đường phụ ïhay dùng, vì nhờ đó mà tạo thành được các cặp đoạn thẳng tỉ lệ B. Các ví dụ: 1) Ví dụ 1: Trên các cạnh BC, CA, AB của tam giác ABC, lấy tương ứng các điểm P, Q, R sao cho ba đường thẳng AP, BQ, CR cắt nhau tại một điểm. Chứng minh: (Định lí Cê – va) Giải Qua A kẻ đường thẳng song song với BC cắt các đường thẳng CR, BQ tại E, F. Gọi O là giao điểm của AP, BQ, CR ARE BRC (a) BOP FOA (1) POC AOE (2) Từ (1) và (2) suy ra: (b) AQF CQB (c) Nhân (a), (b), (c) vế theo vế ta có: * Đảo lại: Nếu thì bai đường thẳng AP, BQ, CR đồng quy 2) Ví dụ 2: Một đường thăng bất kỳ cắt các cạnh( phần kéo dài của các cạnh) của tam giác ABC tại P, Q, R. Chứng minh rằng: (Định lí Mê-nê-la-uýt) Giải: Qua A kẻ đường thẳng song song với BC cắt PR tại E. Ta có RAE RBP (a) AQE CQP (b) Nhân vế theo vế các đẳng thức (a) và (b) ta có (1) Nhân hai vế đẳng thức (1) với ta có: Đảo lại: Nếu thì ba điểm P, Q, R thẳng hàng 3) Ví dụ 3: Cho tam giác ABC, trung tuyến AM. Gọi I là điểm bất kỳ trên cạnh BC. Đường thẳng qua I song song với AC cắt AB ở K; đường thẳng qua I song song với AB cắt AC, AM theo thứ tự ở D, E. Chứng minh DE = BK Giải Qua M kẻ MN // IE (N AC).Ta có: (1) MN // IE, mà MB = MC AN = CN (2) Từ (1) và (2) suy ra (3) Ta lại có (4) Từ (4) và (5) suy ra (a) Tương tự ta có: (6) Vì KI // AC, IE // AC nên tứ giác AKIE là hình bình hành nên KI = AE (7) Từ (6) và (7) suy ra (b) Từ (a) và (b) suy ra DE = BK 4) Ví dụ 4: Đường thẳng qua trung điểm của cạnh đối AB, CD của tứ giác ABCD cắt các đường thẳng AD, BC theo thứ tự ở I, K. Chứng minh: IA . KC = ID. KB Giải Gọi M, N theo thứ tự là trung điểm của AB, CD Ta có AM = BM; DN = CN Vẽ AE, BF lần lượt song song với CD AME = BMF (g.c.g) AE = BF Theo định lí Talét ta có: (1) Củng theo định lí Talét ta có: (2) Từ (1) và (2) suy ra IA . KC = ID. KB 5) Ví dụ 5: Cho , các điểm A, B theo thứ tự chuyển động trên các tia Ox, Oy sao cho (k là hằng số). Chứng minh rằng AB luôn đi qua một điểm cố định Giải Vẽ tia phân giác Oz của cắt AB ở C. vẽ CD // OA (D OB) COD cân tại D DO = DC Theo định lí Talét ta có (1) Theo giả thiết thì (2) Từ (1) và (2) suy ra CD = k , không đổi Vậy AB luôn đi qua một điểm cố định là C sao cho CD = k và CD // Ox , D OB 6) Ví dụ 6: Cho điểm M di động trên đáy nhỏ AB của hình thang ABCD, Gọi O là giao điểm của hai cạnh bên DA, CB. Gọi G là giao điểm của OA và CM, H là giao điểm của OB và DM. Chứng minh rằng: Khi M di động trên AB thì tổng không đổi Giải Qua O kẻ đường thẳng song với AB cắt CM, DM theo thứ tự ở I và K. Theo định lí Talét ta có: ; (1) Qua M vẽ đường thẳng vuông góc với AB cắt IK, CD theo thứ tự ở P và Q, ta có: không đổi vì FO là khoảng cách từ O đến AB, MQ là đường cao của hình thang nên không đổi (2) Từ (1) và (2) suy ra không đổi 7) Ví dụ 7: Cho tam giác ABC (AB < AC), phân giác AD. Trên AB lấy điểm M, trên AC lấy điểm N sao cho BM = CN, gọi giao điểm của CM và BN là O, Từ O vẽ đường thẳng song song với AD cắt AC, AB tại E và F. Chứng minh rằng: AB = CF; BE = CA Giải. AD là phân giác nên EI // AD (góc đồng vị) Mà (đồng vị); (đối đỉnh) Suy ra AFE cân tại A AE =AF (a) Aùp dụng định lí Talét vào ACD , với I là giao điểm của EF với BC ta có (1) AD là phân giác của nên (2) Từ (1) và (2) suy ra (3) Kẻ đường cao AG của AFE . BP // AG (P AD); CQ // AG (Q OI) thì = 900 Gọi trung điểm của BC là K, ta có BPK = CQK (g.c.g) CQ = BP BPD = CQI (g.c.g) CI = BD (4) Thay (4) vào (3) ta có CF = BA (b) Từ (a) và (b) suy ra BE = CA Bài tập về nhà 1) Cho tam giác ABC. Điểm D chia trong BC theo tỉ số 1 : 2, điểm O chia trong AD theo tỉ số 3 : 2. gọi K là giao điểm của BO và AC. Chứng minh rằng không đổi 2) Cho tam giác ABC (AB > AC). Lấy các điểm D, E tuỳ ý thứ tự thuộc các cạnh AB, AC sao cho BD = CE. Gọi giao điểm của DE, BC là K, chứng minh rằng : Tỉ số không đổi khi D, E thay đổi trên AB, AC (HD: Vẽ DG // EC (G BC).
Tài liệu đính kèm:
 cac_chuyen_de_on_thi_hoc_sinh_gioi_mon_toan_lop_8_chuyen_de.docx
cac_chuyen_de_on_thi_hoc_sinh_gioi_mon_toan_lop_8_chuyen_de.docx



