Giáo án Hình học Lớp 8 - Bài 2: Hình thang
A. KIẾN THỨC TRỌNG TÂM
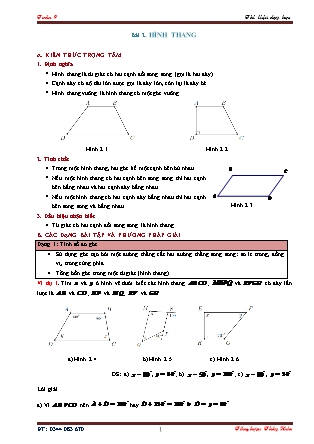
1. Định nghĩa
Hình thang là tứ giác có hai cạnh đối song song (gọi là hai đáy).
Cạnh đáy có độ dài lớn được gọi là đáy lớn, còn lại là đáy bé.
Hình thang vuông là hình thang có một góc vuông.
2. Tính chất
Trong một hình thang, hai góc kề một cạnh bên bù nhau.
Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau.
Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
3. Dấu hiệu nhận biết
Tứ giác có hai cạnh đối song song là hình thang.
Bạn đang xem tài liệu "Giáo án Hình học Lớp 8 - Bài 2: Hình thang", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Bài 2. HÌNH THANG A. KIẾN THỨC TRỌNG TÂM 1. Định nghĩa Hình thang là tứ giác có hai cạnh đối song song (gọi là hai đáy). Cạnh đáy có độ dài lớn được gọi là đáy lớn, còn lại là đáy bé. Hình thang vuông là hình thang có một góc vuông. Hình 2.1 Hình 2.2 2. Tính chất Trong một hình thang, hai góc kề một cạnh bên bù nhau. Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau. Hình 2.3 Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau. 3. Dấu hiệu nhận biết Tứ giác có hai cạnh đối song song là hình thang. B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI Dạng 1: Tính số đo góc Sử dụng góc tạo bởi một đường thẳng cắt hai đường thẳng song song: so le trong, đồng vị, trong cùng phía. Tổng bốn góc trong một tứ giác (hình thang). Ví dụ 1. Tìm và ở hình vẽ dưới biết các hình thang ; và có đáy lần lượt là và ; và ; và . a) Hình 2.4 b) Hình 2.5 c) Hình 2.6 ĐS: a) , ; b) , ; c) , . Lời giải a) Vì nên hay . Tương tự, . b) Ta có . . Vì nên . Tương tự, c) Vì nên . Tương tự . Ví dụ 2. Cho hình thang có hai đáy là và . Biết và . Tính các góc của hình thang. ĐS: ; ; ; . Lời giải Vì nên ; Theo đề bài nên ,. Vì nên mà nên , . Dạng 2: Chứng minh tứ giác là hình thang Sử dụng dấu hiệu nhận biết hình thang. Ví dụ 3. Tứ giác có và là phân giác của góc . Chứng minh là hình thang. Lời giải Xét có nên cân tại suy ra mà là phân giác của nên . Suy ra nên hay là hình thang. Dạng 3: Chứng minh các tính chất hình học Sử dụng tính chất hình thang để chứng minh các yếu tố khác của hình học. Ví dụ 4. Cho hình thang , biết , lần lượt là phân giác của , của hình thang. Chứng minh . Lời giải Gọi . Vì . . Vậy . Ví dụ 5. Cho hình thang (, ). Qua kẻ đường thẳng song song với cắt tại . Chứng minh a) , ; b) ; c) . Lời giải a) Hình thang có hai cạnh bên ; . b) Ta có . c) Áp dụng bất đẳng thức tam giác cho . Mà , nên . C. BÀI TẬP VẬN DỤNG Bài 1. Cho hình thang () có , . Tính các góc của hình thang. ĐS: , , , . Lời giải Vì là hình thang nên ; Mà nên ta tìm được , . Tương tự, ta có và nên , . Bài 2. Cho hình thang () có . Tính số đo và . ĐS: , . Lời giải Ta có nên mà nên . Vậy , . Bài 3. Cho hình thang có , cm, cm. Tính các góc của hình thang. ĐS: , . Lời giải Kẻ (). là hình thang có hai cạnh bên nên cm; cm, suy ra cm. Khi đó vuông cân tại , . Bài 4. Tứ giác có và là phân giác của . Chứng minh là hình thang. Lời giải Xét có nên cân tại suy ra mà là phân giác của nên . Suy ra và hai góc này ở vị trí so le trong nên hay là hình thang. Bài 5. Cho hình thang () có . Gọi là điểm thuộc đáy sao cho . Chứng minh a) là phân giác của ; b) ; c) là phân giác của . Lời giải a) Ta có nên cân tại . Vì nên (hai góc so le trong). Vậy hay là phân giác của . b) Vì mà nên . c) Ta có nên cân tại . Vì nên (hai góc so le trong). Vậy hay là phân giác của . D. BÀI TẬP VỀ NHÀ Bài 6. Cho tam giác có , đường phân giác . Đường vuông góc với tại cắt và lần lượt tại và . Trên cạnh lấy điểm sao cho . Chứng minh là hình thang. Lời giải là phân giác và là đường cao của . cân tại . là đường trung tuyến. . Hình 2.9 Xét và có (giả thiết); (đối đỉnh); (chứng minh trên). (c.g.c). . là hình thang. Bài 7. Cho tam giác . Các tia phân giác của và cắt nhau ở . Qua kẻ đường thẳng song song với , cắt các cạnh và ở và . a) Tìm các hình thang trong hình vẽ. b) Chứng minh và là các tam giác cân. c) Chứng minh . Lời giải a) Các hình thang trong hình vẽ là , , . Hình 2.12 b) nên cân tại . Tương tự cân tại . c) . Bài 8. Cho hình thang (, ). Hai tia phân giác của góc và cắt nhau tại thuộc đáy . Chứng minh a) cân ở , cân ở ; b) . Lời giải a) Vì (hai góc so le trong). (1) là tia phân giác của nên Hình 2.13 . (2) Từ (1) và (2) suy ra hay cân tại . Tương tự (hai góc so le trong) mà nên hay cân tại . b) cân tại nên . cân tại nên . Vậy . --- HẾT ---
Tài liệu đính kèm:
 giao_an_hinh_hoc_lop_8_bai_2_hinh_thang.docx
giao_an_hinh_hoc_lop_8_bai_2_hinh_thang.docx



