Giáo án Hình học Lớp 8 - Chủ đề 2: Hình thang
Chủ đề 2 HÌNH THANG
A. KIẾN THỨC CẦN NHỚ
I. HÌNH THANG
1. Định nghĩa
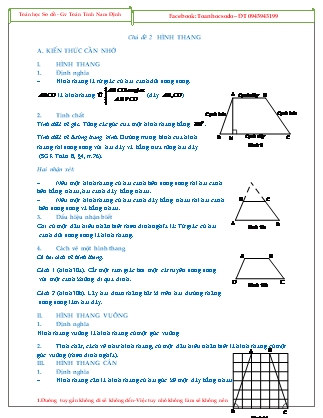
Hình thang là tứ giác có hai cạnh đối song song.
là hình thang (đáy )
2. Tính chất
Tính chất về góc: Tổng các góc của một hình thang bằng .
Tính chất về đường trung bình: Đường trung bình của hình
thang thì song song với hai đáy và bằng nửa tổng hai đáy
(SGK Toán 8, §4, tr.76).
Hai nhận xét:
Nếu một hình thang có hai cạnh bên song song thì hai cạnh
bên bằng nhau, hai cạnh đáy bằng nhau.
Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh
bên song song và bằng nhau.
3. Dấu hiệu nhận biết
Chỉ có một dấu hiệu nhận biết theo định nghĩa là: Tứ giác có hai
cạnh đối song song là hình thang.
Bạn đang xem tài liệu "Giáo án Hình học Lớp 8 - Chủ đề 2: Hình thang", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Facebook :Toanhocsodo – ĐT 0945943199 Toán học Sơ đồ - Gv Toán Tỉnh Nam Định Chủ đề 2 HÌNH THANG A. KIẾN THỨC CẦN NHỚ HÌNH THANG Định nghĩa Hình thang là tứ giác có hai cạnh đối song song. là hình thang (đáy ) Tính chất Tính chất về góc: Tổng các góc của một hình thang bằng . Tính chất về đường trung bình: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy (SGK Toán 8, §4, tr.76). Hai nhận xét: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau. Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau. Dấu hiệu nhận biết Chỉ có một dấu hiệu nhận biết theo định nghĩa là: Tứ giác có hai cạnh đối song song là hình thang. Cách vẽ một hình thang Có hai cách vẽ hình thang: Cách 1 (hình 10a). Cắt một tam giác bởi một cát tuyến song song với một cạnh không đi qua đỉnh. Cách 2 (hình 10b). Lấy hai đoạn thẳng bất kì trên hai đường thẳng song song làm hai đáy. HÌNH THANG VUÔNG Định nghĩa Hình thang vuông là hình thang có một góc vuông Tính chất, cách vẽ như hình thang, có một dấu hiệu nhận biết là hình thang có một góc vuông (theo định nghĩa). HÌNH THANG CÂN Định nghĩa Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Tứ giác là hình thang cân . Tính chất Ngoài các tính chất của hình thang, hình thang cân còn có: Tính chất về cạnh bên: Trong hình thang cân, hai cạnh bên bằng nhau. Tính chất về đường chéo: Trong hình thang cân, hai đường chéo bằng nhau. Dấu hiệu nhận biết Có hai dấu hiệu nhận biết hình thang cân Hình thang có hai góc kề một đáy bằng nhau là hình thang cân. Hình thang có hai đường chéo bằng nhau là hình thang cân. 4. Cách vẽ một hình thang cân Cách 1 (hình 12a). Cắt một tam giác cân bởi một cát tuyến song song với đáy. Cách 2 (hình 12b). Trên một trong hai đường thẳng song song và . Chẳng hạn là , chọn một đoạn thẳng . Lấy và làm tâm quay hai đường tròn tâm và có cùng bán kính cắt đường thẳng tại bốn đểm theo thứ tự ta được là hai hình thang cân như hình 30, hình 31 (SGK Toán 8, Tập 1 - tr. 74, 75). IV. PHÂN TÍCH ĐI LÊN ĐỂ TÌM KIẾM LỜI GIẢI CHO CÁC CHỨNG MINH ĐỊNH LÍ CỦA CHỦ ĐỀ 2 Học sinh tập phân tích đi lên, vẽ hình, viết lời giải rồi so sánh với lời giải trong SGK. 1. Định lí: Tổng các góc của một tứ giác bằng . Chứng minh Xét tứ giác như hình 13. Ta phải chứng minh: 2. Định lí: Trong hình thang cân hai cạnh bên bằng nhau. Chứng minh Xét hình thang cân , ta phải chứng minh . Xét hai trường hợp: a) cắt ở (giả sử ). Dùng lưới ô vuông để vẽ hình (h.14) Phân tích: . b) . Dùng lưới ô vuông để vẽ hình (h.15). Phân tích: Hình thang có hai cạnh bên song song (theo nhận xét về hình thang). 3. Định lí: Trong hình thang cân, hai đường chéo bằng nhau. Chứng minh Xét hình thang cân . Ta phải chứng minh . Dùng lưới ô vuông để vẽ hình (h.16). Phân tích: (tính chất hình thang cân). B. CÁC DẠNG BÀI TẬP CƠ BẢN DẠNG 1. Nhận biết hình thang. Hình thang vuông. Hình thang cân I. PHƯƠNG PHÁP GIẢI Sử dụng: Định nghĩa hình thang, hình thang vuông, hình thang cân. Hình thang có hai đường chéo bằng nhau là hình thang cân. II. VÍ DỤ Ví dụ 1. Tứ giác có và là tia phân giác của góc . Chứng minh rằng là hình thang. Lời giải (hình 17) Từ giả thiết suy ra tam giác cân ở . Áp dụng tính chất về góc và giả thiết vào tam giác cân, ta được: . Vì có cặp góc so le trong bằng nhau. Tứ giác có hai cạnh đối song song nên nó là hình thang. Ví dụ 2. Cho tam giác vuông cân tại . Vẽ ra phía ngoài của tam giác một tam giác vuông cân tại . Tứ giác là hình gì? Tại sao? Lời giải (hình 18) Từ giả thiết tam giác vuông cân ở , vuông cân ở . Nên các góc ở đáy do có cặp góc so le trong bằng nhau. Tứ giác có hai cạnh đối song song nên nó là hình thang. Hình thang lại có theo giả thiết nên nó là hình thang vuông. Ví dụ 3. Hình thang có . Chứng minh rằng là hình thang cân. Lời giải (hình 19) Áp dụng tính chất góc so le của và giả thiết, ta có: (Vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau). Cộng theo vế các đẳng thức (1) và (2) thu được . Điều này chứng tỏ hình thang có hai đường chéo bằng nhau nên nó là hình thang cân. Ví dụ 4. Cho hình thang có . Qua kẻ đường thẳng song song với , cắt đường thẳng tại . Chứng minh rằng: a) là tam giác cân. b) . c) Hình thang là hình thang cân. Lời giải (hình 20) a) Áp dụng nhận xét hình thang có hai cạnh bên song song và giả thiết vào hình thang , thu được: . Tam giác có hai cạnh bằng nhau nên nó cân tại . b) Áp dụng tính chất về góc vào tam giác cân và tính chất góc đồng vị của , ta được: . (1) Lại có (theo giả thiết) (2) Có . (3) Từ (1), (2) và (3) suy ra (c-g-c). c) Hình thang có hai đường chéo bằng nhau nên nó là hình thang cân. III. BÀI TẬP 1. Chứng minh rằng nếu cắt hai cạnh của một tam giác cân bởi một cát tuyến song song với cạnh đáy thì tứ giác thu được là một hình thang cân. 2. Cho tam giác cân tại . Kẻ các đường trung tuyến . Tứ giác là hình gì? Vì sao? 3. Cho cân tại . Kẻ các đường cao . Tứ giác là hình gì? Vì sao? 4. Hai đoạn thẳng và cắt nhau tại , biết rằng . Tứ giác là hình gì? Vì sao? 5. Cho tam giác cân tại . Lấy điểm trên cạnh , điểm trên cạnh sao cho . a) Tứ giác là hình gì? Vì sao? b) Các điểm ở vị trí nào thì ? 6*. Một hình thang có hai cạnh bên bằng nhau có phải là hình thang cân không? Phải bổ sung thêm điều kiện gì thì hình thang có hai cạnh bên bằng nhau là hình thang cân? DẠNG 2. Tính góc của hình thang I. PHƯƠNG PHÁP GIẢI Sử dụng: Tính chất về góc của một tam giác, tứ giác. Tính chất hai góc trong cùng phía của hai đường thẳng song song bù nhau. Định nghĩa hình thang cân. II. VÍ DỤ Ví dụ 1. Hình thang có . Tính các góc của hình thang. Lời giải (hình 21) Áp dụng tính chất các góc trong cùng phía của và giả thiết, ta được: Cộng theo vế các đẳng thức (1) và (2), ta được: hay , suy ra . Trừ theo vế các đẳng thức (3) và (4), ta được: hay , suy ra . Ví dụ 2. Hình thang vuông có ; . Tính góc và của hình thang. Lời giải (hình 22) Kẻ thì , do cùng vuông góc với nên hình thang có hai cạnh bên song song. Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang và giả thiết ta được , do đó: . Suy ra vuông cân tại nên . Do góc và là hai góc trong cùng phía của nên chúng bù nhau hay , suy ra . Ví dụ 3. Tính các góc của hình thang cân, biết một góc bằng . Lời giải (hình 23) Xét hình thang cân có . Theo định nghĩa hình thang cân và giả thiết ta có và . Do góc và là hai góc trong cùng phía của nên chúng bù nhau hay . nên . Ví dụ 4. Cho cân tại . Lấy điểm trên cạnh , điểm trên cạnh sao cho . a) Chứng minh rằng là hình thang cân. b) Tính các góc của hình thang cân đó, biết rằng . Lời giải (hình 24) a) Từ giả thiết nên tam giác cân ở . Đặt . Áp dụng tính chất về góc vào hai tam giác cân và , ta được: (vì có cặp góc đồng vị bằng nhau). Tứ giác có hai cạnh đối song song nên nó là hình thang. Hình thang này lại có hai góc kề một đáy bằng nhau là nên là hình thang cân. b) Áp dụng kết quả của câu a) với hay , ta được: . Do các góc và là các cặp góc trong cùng phía của nên chúng bù nhau, suy ra . III. BÀI TẬP 7. a) Biết ít nhất mấy góc của một hình thang thì tính được các góc còn lại? b) Biết hai góc của một hình thang bằng và . Tính các góc còn lại của hình thang. 8. Cho biết hai góc đối của hình thang là và . Tính các góc còn lại. 9. Hình thang có và . Tính các góc còn lại. 10. a) Biết ít nhất mấy góc của một hình thang cân thì tính được các góc còn lại? b) Một hình thang cân có một góc bằng . Đó là góc ở đáy lớn hay đáy nhỏ? Tính các góc còn lại. 11. Hai góc của một hình thang cân có hiệu bằng . Đó là hai góc ở một đáy hay hai góc ở một cạnh bên? Tính các góc của hình thang. DẠNG 3. Chứng minh quan hệ về độ dài. Tính độ dài đoạn thẳng I. PHƯƠNG PHÁP GIẢI 1. Chứng minh quan hệ về độ dài Sử dụng: Tính chất về cạnh bên và đường chéo của hình thang cân. Trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau và ngược lại. 2. Tính độ dài đoạn thẳng Chọn tam giác vuông thích hợp chứa đoạn thẳng rồi áp dụng định lí Py-ta-go. II. VÍ DỤ Ví dụ 1. Cho hình thang cân . Kẻ các đường cao của hình thang. Chứng minh rằng . Lời giải (hình 25) Áp dụng định nghĩa, tính chất và giả thiết vào hình thang cân , ta được: (trường hợp cạnh huyền - góc nhọn). Vậy . Ví dụ 2. Cho hình thang cân có là giao điểm của hai đường chéo. Chứng minh rằng: và . Lời giải (hình 26) Áp dụng tính chất về cạnh bên và đường chéo vào hình thang cân , ta được: (c-c-c) Suy ra (vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau). (2) Trừ theo vế các đẳng thức (1) và (2), ta được . Ví dụ 3. Cho hình thang hai đường phân giác của góc và cắt nhau tại điểm thuộc đáy . Chứng minh rằng tổng hai cạnh bên bằng đáy của hình thang. Lời giải (hình 27) Áp dụng tính chất góc so le của và giả thiết, ta có: (vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau). Cộng theo vế các đẳng thức (1) và (2) ta được . Điều này chứng tỏ tổng hai cạnh bên bằng đáy của hình thang. Ví dụ 4*. Tính chiều cao của hình thang cân , biết rằng cạnh bên , các cạnh đáy và . Lời giải (hình 28) Kẻ thì nên hình thang có hai cạnh bên song song. Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang , ta được: . Áp dụng định lí Py-ta-go vào tam giác vuông tại , thu được: hay vì . Vậy chiều cao của hình thang cân là . Ví dụ 5*. Tính chiều cao của hình thang cân , biết và hai cạnh đáy . Từ đó suy ra cách vẽ hình. Lời giải (hình 29) Kẻ cắt tại thì , do cùng vuông góc với . Hình thang có hai cạnh bên song song, nên (1) và hai đáy . Suy ra . Lại có (tính chất đường chéo của hình thang cân). (2) Từ (1) và (2) suy ra nên tam giác vuông cân tại . Do đó vừa là đường cao vừa là đường trung tuyến của tam giác , nên và , lúc đó tam giác vuông cân tại . Vậy . Cách vẽ hình: Bước 1: Vẽ vuông cân tại có đường cao và . Bước 2: Kẻ . Lấy sao cho . Bước 3: Kẻ cắt tại . Ta được hình thang cân thoả mãn yêu câu của đầu bài. III. BÀI TẬP 12. Kéo dài hai cạnh bên của một hình thang cân (có hai đáy không bằng nhau) thì tam giác thu được có phải là tam giác cân hay không? Vì sao? 13. Cho hình thang cân có hai đường chéo cắt nhau tại , các cạnh bên kéo dài cắt nhau tại . Chứng minh rằng đường thẳng là đường trung trực của hai đáy. 14. Một hình thang cân có đáy lớn dài , cạnh bên dài , góc tạo bởi cạnh bên và đáy lớn bằng . Tính độ dài của đáy nhỏ. 15. Hình thang cân có đường chéo vuông góc với cạnh bên và là tia phân giác của góc . Tính chu vi của hình thang, biết . ------///---------
Tài liệu đính kèm:
 giao_an_hinh_hoc_lop_8_chu_de_2_hinh_thang.docx
giao_an_hinh_hoc_lop_8_chu_de_2_hinh_thang.docx



