Giáo án dạy thêm Hình học Lớp 8 - Bài 7: Trường hợp đồng dạng thứ ba (G.G)

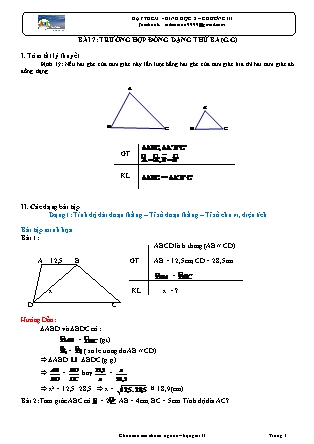
BÀI 7: TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA (G.G)
I. Tóm tắt lý thuyết
Định lý: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
GT
KL
II. Các dạng bài tập
Dạng 1: Tính độ dài đoạn thẳng – Tỉ số đoạn thẳng – Tỉ số chu vi, diện tích
Bài tập minh họa 
Bài 1:
	ABCD là h.thang (AB // CD)
 A 12,5 B 	 GT	AB = 12,5cm; CD = 28,5cm
	 = 
	 x	 KL	 x = ?
 D C 
Hướng Dẫn:
DABD và DBDC có : 
 = (gt)
	 = ( so le trong do AB // CD)
Þ DABD DBDC (g.g)
Þ = hay = 
Þ x2 = 12,5 . 28,5 Þ x = » 18,9(cm)
Bài 2: Tam giác ABC có = 2; AB = 4cm; BC = 5cm. Tính độ dài AC?
Hướng Dẫn:
 A	
 	Trên tia đối của tia BA lấy BD = BC
 B	 DACD và DABC có chung; = = µ
 	 	Þ DACD DABC (g.g)
Þ = Þ AC2 = AB. AD
D C	 = 4 . 9 = 36
Þ AC = 6(cm)
Bài 3: Cho DABC, D là điểm trên cạnh AC sao cho . Biết AD = 7cm; DC = 9cm. Tính tỷ số 
	 B	DABC; D Î AC : ;
	GT	AD = 7cm; DC = 9cm	 	 KL	Tính .
 C D A
Hướng Dẫn:
DCAB và DCDB có C chung ; = (gt)
Þ DCAB DCDB (g.g) Þ do đó ta có : 
	CB2 = CA.CD
Theo gt CD = 9cm; DA = 7cm nên CA = CD + DA = 9 + 7 = 16 (cm)
Do đó CB2 = 9.16 = 144 Þ CB = 12(cm)
Mặt khác lại có : 
Bài 4:Cho hình vuông ABCD, gọi E và F theo thứ tự là trung điểm của Ab, BC, CE cắt DF ở M. Tính tỷ số ?
 D C 	Hình vuông ABCD; AE = EB ;
 M	GT	BF = CF; CE Ç DF tại M	 	 F 	 KL	Tính ?
 A E B 
Hướng Dẫn:
Xét DDCF và DCBE có DC = BC (gt); = = 900; BE = CF
DDCF = DCBE (c.g.c) Þ 1 = 2
Mà 1 + 2 = 1v Þ 1 + 1 = 1v Þ DCMD vuông ở M
DCMD DFCD (vì 1 = 2 ; = ) Þ 
 = Þ SCMD = . SFCD
Mà SFCD = CF.CD = .BC.CD = CD2
Vậy SCMD = . CD2 = . (*)
Áp dụng định lý pitago vào tam giác vuông DFC, ta có:
DF2 = CD2 + CF2 = CD2 + (BC)2 = CD2 + CD2 = CD2
Thay DF2 = CD2 ta có :
	SCMD = CD2 = SABCD
	Þ = 
Bài 5: 
Hướng Dẫn:
	 DABC ( = 900); AH ^ BC
	GT BM = CM; BH = 4cm; CH = 9cm	 	 KL	Tính SDAMH
 A
Xét 2D vuông HBA và D vuông HAC có : 
 + = 1v (1)
	 + = 1v (2)
Từ (1) và (2) Þ = 
Vậy DHBA D HAC (g.g)	B 4 H M C
Þ Þ HA2 = HB.HC = 4.9 = 36 9
	Þ HA = 6cm
Lại có BC = BH + HC = 4cm + 9cm = 13cm
SDABM = SDABC = . = 19,5(cm2)
SDAHM = SDBAH = 19,5 - .4.6 = 7,5(cm2)
Vậy SDAMH = 7,5(cm2)
Bài 6:Cho DABC và hình bình hành AEDF có E Î AB; D Î BC, F Î AC. Tính diện tích hình bình hành biết rằng : SEBD = 3cm2; SFDC = 12cm2;
	 DABC hình bình hành AEDF
	GT SEBD = 3cm2; SFDC = 12cm2	 	 KL	Tính SAEDF
Hướng Dẫn:
Xét DEBD và DFDC có = 1 (đồng vị do DF // AB) (1)
Þ 1 = 1 (2)
E1 = D2 ( so le trong do AB // DF)
D2 = E1 ( so le trong do DE // AC) 
Từ (1) và (2) Þ DEBD DFDC (g.g)
Mà SEBD : SFDC = 3 : 12 = 1 : 4 = ()2
Do đó : Þ FD = 2EB và ED = FC A
Þ AE = DF = 2BE ( vì AE = DF) F
AF = ED = EC ( vì AF = ED) E 1 
Vậy SADE = 2SBED = 2.3 = 6(cm2) 1 2
SADF = SFDC = . 12 = 6(cm2) B D C 
Þ SAEDF = SADE + SADF = 6 + 6 = 12(cm2)
Dạng 2:Chứng minh hai tam giác đồng dạng
Phương pháp giải: Chỉ ra hai cặp góc tương ứng bằng nhau trong hai tam giác để suy ra hai tam giác đồng dạng.
Bài tập minh họa 
Bài 1: B
F
D
A
E
 3,6
 C
 2,4
Cho DABC; AB = 4,8cn; AC = 6,4cm; BC = 3,6cm
Trên AB lấy điểm D sao cho AD = 3,2cm, trên AC 
lấy điểm E sao cho AE = 2,4cm, kéo dài ED cắt CB ở F.
CMR : D ABC DAED
DFBD DFEC
Tính ED ; FB?
Hướng Dẫn: 
Sơ đồ chứng minh:
a) 	 GT
 	 ß
	 chung 
	 = = 2
 ß
DABC DAED (c.g.c)
DABC D AED (câu a)
b) ß
	 = ; = 	
 ß
	 = 
	 chung
 ß
DFBD DFEC (g.g)
c)Từ câu a, b hướng dẫn học sinh thay vào tỷ số đồng dạng để tính ED và FB.
A
E
C
M
B
D
1
1
Bài 2:Cho DABC cân tại A; BC = 2a; M là trung điểm của BC. Lấy các điểm D và E trên AB; AC sao cho = .
a) CMR : DBDM DCME
b) DMDE DDBM
c) BD . CE không đổi 
Hướng dẫn: 
gt	góc ngoài DDBM
 ß ß
 = ; = + ; = + 
DABC cân 
 ß 	 ß
 = 	; 	 = 
 ß
DBDM DCME (gg)
Câu a	 gt
 ß ß
b)	 = ; CM = BM
 ß
 = 
 ß
 = (gt) ; 
 ß
	DDME DDBM (c.g.c)
c) Từ câu a : DBDM DCME (gg)
Þ Þ BD . CE = Cm . BM
Mà CM = BM = = a
Þ BD . CE = (không đổi)
Bài 3: Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB, cắt tia AD tại E. Chứng minh:
a) 	b) cân tại C.
Hướng Dẫn:
a) Do AB//CE nên . Chứng minh được 
b) Chứng minh được nên cân tại C.
Bài 4: Hình thang ABCD , có .Chứng minh 
Hướng Dẫn:
Chứng minh được 
Bài 5: Cho có AM là phân giác của . Kẻ tia Cx thuộc nửa mặt phẳng bờ BC không chứa A sao cho Gọi N là giao của Cx và tia AM. Chứng minh:
a) 	b) 
c) Tam giác BCN cân.
Hướng Dẫn:
a) Chứng minh được Þ ĐPCM.
b) Từ a, suy ra . Từ đó chứng minh được 
c) Từ a, có .
Chứng minh được .Do đó , ta chỉ ra Þ ĐPCM.
Bài 6: Cho hình bình hành ABCD. Một cát tuyến d qua A bất kì cắt đường chéo BD tại E và các đường thẳng BC, CD lần lượt tại F và G. Chứng minh:
a) 	b) 
c) và tích số luôn không đổi khi d quay quanh A.
Hướng Dẫn:
a) b) HS tự chứng minh.
c) Sử dụng tính chất bắc cầu, ta chỉ ra được . Từ đó suy ra BF.DG = AB.AD, mà AB.AD không đổi khi d quay quanh A Þ ĐPCM.
Dạng 3: Sử dụng các trường hợp đồng dạng thứ ba để tính độ dài các cạnh, chứng minh hệ thức cạnh hoặc chứng minh các góc bằng nhau
Phương pháp giải: Sử dụng trường hợp đồng dạng thứ ba (nếu cần) để chứng minh hai tam giác đồng dạng, từ đó suy ra các cặp góc tương ứng bằng nhau hoặc cặp cạnh tương ứng tỉ lệ.
Bài tập minh họa 
Bài 1: Cho hình thang ABCD(AB // CD). Gọi O là giao điểm của 2đường chéo AC và BD
a)Chứng minh rằng: OA. OD = OB. OC.
b)Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K. CMR: = 
Hướng Dẫn:
	a) OA. OD = OB.OC
Phân tích Sơ đồ hướng chứng minh:
D
K
C
B
H
O
A
	+ 1 = 1 (SLT l AB // CD)
	+ = ( Đối đỉnh) 
ß 
	 DOAB DOCD (g.g) 
ß	
	 = 
ß
	 OA.OD = OC.OC
Học sinh tự trình bày theo sơ đồ đi lên
b) = 
Phân tích Sơ đồ hướng chứng minh:
	+ = = 900
	+ 1 = 1.(SLT; AB // CD)	Câu a
ß	 ß
	DOAH P OCK(gg)	 DOAB DOCD
ß	 ß
	 = 	 = 
	 = 
	Học sinh tự trình bày lại theo sơ đồ đi lên
Bài 2: Cho hai tam gíac vuông ABC và ABD có đỉnh góc vuông C và D nằm trên cùng một nửa mặt phẳng bờ AB. Gọi P là giao điểm của các cạnh AC và BD. Đường thẳng qua P vuông góc với AB tại I. CMR : AB2 = AC. AP + BP.PD 
P6
 O C 
 A I B
Hướng Dẫn:
Xét đoạn thẳng AB (AB = AI + IB)
Þ AB2 = ? 	(AB.(AI + IB) = AB . AI + AB. IB)
Việc chứng minh bài toán trên đưa về việc chứng minh các hệ thức
	AB.AI = AC.AP
	AB.IB = BP.PD
Sơ đồ chứng minh:
 + = = 900	 + = = 900
+ chung 	+ chung 
 ß ß
DADB DPIB	DACB DAIP (gg)
 ß ß
 = 	 = 
 ß ß
AB.AI = PB.DB	AB . AI = AC . AP
AB . IB + AB . AI = BP . PD + AC . AP
 	 ß
AB (IB + IA) = BP . PD + AC . AP
 ß
AB2 = BP . PD + AC . AP
	Học sinh tự trình bày lại theo sơ đồ đi lên
Bài 3: Cho D ABC, I là giao điểm của 3 đường phân giác, đường thẳng vuông góc với CI tại I cắt AC và BC lần lượt ở M và N. Chứng minh rằng.
I
a) AM . BI = AI. IM	 A
b) BN . IA = BI . NI 	M	 
c) = 	 
Hướng Dẫn : 
a) Để chứng minh hệ thức AM. BI = AI. B N C
IM ta cần chứng minh: 
b) Để chứng minh đẳng thức trên ta cần chứng minh: (D AMI DAIB)
Sơ đồ: 
 = (gt)	 = 	* CM: = 
	DMIC vuông: = 900 - 
	DAMI DAIB (gg)	DABC: + 	 + = 1800(t/c tổng...)
	 ß	Þ + + = 900
	 = 	Do đó: = + (1)
	 ß	Mặt khác: = + (t/c góc ngoài D)
	AM. BI = AI . IM	hay = + (2) 
	Từ (1) và (2) Þ = hay = 
DAMI DAIB ( = ; = )
Þ = Þ AM . BI = AI. IM
b) Tương tự ý a.
Chứng minh DBNI P DBIA (gg)
Þ = Þ BN . IA = BI. IN
c)	(Câu a)	(Câu b)
 	 ß 	 ß
Nhận xét = 	 DAMI P DAIB	 DBNI P DBIA
 	 ß 	 ß
Tính AI2 ; BI2 Þ 	 = 	 = 
 	 ß 	 ß
(Tính AI2 ; BI2 nhờ DP)	AI2 = AM . AB	 BI2 = BN . AB 
	 = 
 	 ß
	 = 
Học sinh tự trình bày lại theo sơ đồ đi lên
Bài 4: Cho D ABC có các góc nhọn, kẻ BE, CF là hai đường cao. Kẻ EM, FN là hai đường cao của DAEF. Chứng minh MN // BC
Hướng Dẫn:
Sơ đồ phân tích
DAMF P DAFC (g.g);	DAFN P DABE A
ß	 ß M N
 = 	 = 	 F E
ß 
 . = . B C 
	ß
 = 
ß
MN // BC (định lý Ta – lét đảo)
Bài 5: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:
a) 	b) 
Hướng Dẫn:
a) Chứng minh được 
b) Chứng minh được
Bài 6: Cho tam giác ABC vuông tại A, Q là điểm trên AC. Gọi D là hình chiếu của Q trên BC và E là giao điểm của AB và QD. Chứng minh:
a) 	b) 
Hướng Dẫn:
Bài 7: Cho tam giác ABC , đường phân giác trong AD. Gọi M và N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. Chứng minh:
a) 	b) 
Hướng Dẫn:
a) Chứng minh suy ra 
b) Chứng minh , suy ra 
Từ (1) và (2) Þ ĐPCM.
Bài 8: Cho tam giác ABC , đường phân giác trong AD. Trên tia đối của tia DA lấy điểm I sao cho Chứng minh:
a) 	b) 
c) 
Hướng Dẫn:
a) HS tự chứng minh.
b) HS tự chứng minh.
c) Từ a, suy ra AB.AC = AD.AI (1)
Từ b, suy ra BD.CD = AD.ID (2)
Từ (1) và (2), ta chứng minh được AD2 = AB.AC- DB.DC
III. Bài tập tự luyện
Bài 1: Cho tam giác ABC có AB = 6cm, AC =9cm.Điểm D thuộc cạnh AC sao cho . Tính độ dài AD
Hướng Dẫn:
 Xét DABDvàDACB
chung
.
=>DABD~DACB
Bài 2 :Cho tam giác ABC có AC ≥ AB, đường phân giác AD. Lấy điểm E thuộc cạnh AC sao cho.
a)Tìm tam giác đồng dạng với tam giác ABC.
b)Chứng minh rằng : ED = DB
Hướng Dẫn:
 	Xét DDEC và DABC
chung
DDEC~DABC
 vậy DE=DB
Bài 3 :Cho tam giác ABC và các đường cao BD, CE
a)Chứng minh rằng :DABD~DACE.
b)Tính biết 
Hướng Dẫn:
a) XétDABD và DACE
chung
:DABD~DACE.
b) = 400
Bài 4: Tứ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O , ÐBAO = ÐBDC.Chứng minh;
a)DABO đồng dạng với DDCO
b)DBCO đồng dạng với DADO
Hướng Dẫn:
a/ Xét DABO và DDCO có:
 BÂC = BDC (GT)
 AÔB = DÔC (đối đỉnh)
 	 Nên DABODDCO (g.g) ÞÐB = ÐC (góc t/ứng).
b/ Ta có: ÐC = 900 – ÐC (GT)
	ÐB = 900 – ÐD (Â = 900) ÞÐC = ÐD.
 Mà ÐB = ÐC (ch/m trên)
 	Xét DBCO và DADO có:
	ÐC = ÐD(Ch/m trên)
 BÔC = AÔD (đối đỉnh).
 	 Nên DBCODADO (g.g).
Bai 5: Cho tam giác ABC có . Đặt và Chứng minh 
Hướng Dẫn:
Gợi ý: Kẻ AD là đường phân giác của góc A.
Theo tính chất đường phân giác, 
Chứng minh 
Thay (1) vào (2) được Þ ĐPCM
Bai 6: Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường thẳng song song với AB và BC, lần lượt cắt d tại M và N. Gọi D là giao điểm của ME và BC. Đường thẳng NE cắt AB và MC lần lượt tại F và K. Chứng minh:
a) 	b) 
Hướng Dẫn:
a) Chứng minh BFED là hình bình hành
Chứng minh 
Chứng minh 
Từ (1), (2) và (3) 
Từ đó chứng minh được 
b) Ta chỉ ra được , từ đó suy ra AN//MK
Bai 7: Cho tam giác nhọn ABC có các đường cao AD, BE và CF đồng quy tại H. Chứng minh:
a) ;
b) H là giao điểm các đường phân giác của ;
c) 
Hướng Dẫn:
a) Chứng minh được 
Từ đó chứng minh được 
b) Tương tự câu a, ta có 
Từ a, suy ra nên . Từ đó chứng minh được , suy ra EH là phân giác của 
Chứng minh tương tự ta chỉ ra được H là giao điểm các đường phân giác của 
c) Chứng minh được BD.BC = BH.BE (1)
Chứng minh được CD.BC = CH.CF (2)
Từ (1) và (2), ta có BH.BE + CH.CF = BC2
Bài 8: Cho tam giác ABC có phân giác trong AD. Chứng minh rằng 
Hướng Dẫn:
Trên tia AD lấy điểm E sao cho 
Xét và có (vì AD là phân giác)
 	 do đó 
 (1)
Xét và có
(đối đỉnh)
suy ra 
 (2)
Từ (1) và (2) suy ra: 
Bài 9: Cho tam giác ABC có ba góc nhọn. Gọi M là trung điểm cạnh BC, N là trung điểm cạnh AC. Các đường trung trực của cạnh BC và AC cắt nhau tại điểm O. H là trực tâm và G là trọng tâm.
a) Hai tam giác ABH và MNO đồng dạng?
b) Hai tam giác AHG và MOG đồng dạng?
c) Ba điểm H, G, O thẳng hàng.
Hướng Dẫn:
a) Ta có AH//OM; AB//MN; BH//ON nên
Do đó 
b) Xét hai tam giác OMG và HAG ta có 
Nên 
c) Từ câu b) suy ra .
 	Ta có suy ra H, G, O thẳng hàng
Bài 10: Cho tam giác, đường phân giác AI. Gọi D và E lần lượt là hình chiếu của B và C lên AI. Chứng minh: 
Hướng Dẫn:
Ta có AI là phân giác góc A.
Nên theo tính chất đường phân giác ta có (1)
Ta lại có BD//EC (vì cùng vuông góc với AI) (2)
Từ (1) và (2) suy ra (3)
Mặt khác, xét và có
(AI là phân giác góc A)
Suy ra (g-g)
 (4)
Từ (3) và (4) suy ra 
Bài 11: Tam giác ABC có hai trung tuyến AK và CL cắt nhau tại O. Từ một điểm P bất kỳ trên cạnh AC, vẽ các đường thẳng PE song song với AK, PF song song với CL ( E thuộc BC, F thuộc AB) các trung tuyến Ak, CL cắt đoạn thẳng EF theo thứ tự tại M, N. Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.
L
B
K
E
C
P
A
M
N
O
Hướng Dẫn:
Từ giả thiết cho song song ta suy ra 
các tỷ lệ thức và tam giác đồng dạng
Ta có : 
 = (1) 
 = (cùng )
Þ = (2) ( ta có trung tuyến )
Từ (1) và (2) suy ra : = Þ FM = FE
Tương tự ta cũng có EN = EF và do đó suy ra MN = EF
Vậy FM = MN = NE
Bài 12:Cho hình thang ABCD (AB // CD) đường thẳng song song với đáy Ab cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. CMR: MN = PQ
Hướng Dẫn :
Từ hệ quả của định lý Talet cho ta các tam giác đồng dạng và ta chứng minh được:
D
M
A
B
Q
C
P
N
O
E
	 = 
	 = 
	 = (kéo dài AD cắt BC tại E
rồi chứng minh )
	Þ = Þ MN = PQ
Bài 13: Trên một cạnh của góc xoy ( ¹ 1800), đặt các đoạn thẳng OA = 5cm, OB = 16cm. Trên cạnh thứ nhất của góc đó, đặt các đoạn thẳng OC = 8cm, OD = 10cm.
a) Chứng minh hai tam giác OCB và OAD đồng dạng.
x
y
D
I
C
A
B
b) Gọi giao điểm các cạnh AB và BC là I, CMR: Hai tam giác IAB và IBC có các góc bằng nhau từng đôi một.
 5
 O
 8
 10
a)Þ = 	và Góc O chung
Þ DOBC D ODA	
b)DIAB và DICD ta dễ nhìn thấy không bằng nhau. 
Do đó để chứng minh chúng có các góc bằng nhau từng đôi một ta đi chứng minh đồng dạng.
Vì DOBC P DODA nên = (1)
Mặt khác ta có (đối đỉnh)
Þ DBAI P DDCI (g.g)
Þ 
Bài 14 : Cho tam giác , trực tâm H. Gọi thứ tự là trung điểm của. Các đường trung trực của và của cắt nhau ở .
a) Tìm tam giác đồng dạng với tam giác 
b) Chứng minh rằng 
c) Gọi C là trọng tâm của tam giác. Chứng minh rằng các tam giác và đồng dạng
d) Chứng minh rằng thẳng hàng và 
Hướng Dẫn :
a) Xét và :
 (góc có cạnh tương ứng song song:);
 (góc có cạnh tương ứng song song:)
Vậy và đồng dạng (g.g)
b) và đồng dạng 
suy ra: (vì là đường trung bình của ). Do đó 
c)Ta có mà (tính chất G là trọng tâm của ) nên 
Ta lại có (so le trong, )
Do đó và đồng dạng (c.g.c)
d) và đồng dạng (1)
Ta lại có (2)
Từ (1) và (2) suy ra . 
Do đó thẳng hàng, 
Bài 15 : Tam giác có,. Điểm D thuộc cạnh BC sao cho . Tính độ dài
Hướng Dẫn :
 và đồng dạng (g.g)
 cm
Bài 16 : Hình thang, . Biết. Chứng minh rằng.
Hướng Dẫn :
 và đồng dạng (g.g)
Bài 17 : Trên cùng một tia gốc,ta đặt Trên tia, ta đặt. Các đường tròn và cắt nhau ở E. Chứng minh rằng.
Hướng Dẫn :
Do nên cân; nên . Các tam giác cân có góc đáy là góc chung nên đồng dạng (g.g) suy ra do đó 
Chú ý: bài toán này cho ta một cách dựng đoạn trung bình nhân của hai đoạn thẳng a và b
Bài 18 : Cho điểm thuộc tia. Đường tròn cắt ở . Các đường tròn và cắt nhau ở. Đường tròn cắt ở. Chứng minh rằng là trung điểm của 
Hướng Dẫn :
Đặt thì , . Các tam giác cân có nên đồng dạng (g.g)
Vậy M là trung điểm của AB.
Chú ý: Bài toán này cho ta bài toán dựng hình: Cho điểm B thuộc tia Am. Chỉ dùng compa, dựng trung điểm của AB.
Bài 19 : Tam giáccó các đường trung tuyến sao cho.
 a) Chứng minh rằng tamcân. 
 b)* Chứng minh rằng nếu cho thêm điều kiện thì tam giác đều 
Hướng Dẫn :
a) và đồng dạng (vì)
b)chú ý rằng có và nên chứng minh được (kẻ rồi chứng tỏ rằng trùng ). Do đó . Vậy đều
Bài 20 : a) Cho tam giác có . Chứng minh rằng.
b) Cho tam giác có. Chứng minh rằng 
c) Cho tam giác có,. Tính độ dài.
Hướng Dẫn :
a)Trên tia đối của tia BA lấy điểm D sao cho BD = BC. 
Cách vẽ này vừa làm xuất hiện AD = AB + BC, vừa làm xuất hiện (Vì cân nên ) do đó 
Ta có và đồng dạng (g.g) nên = 
b) Cũng vẽ điểm D như câu a. Ta có nên . 
Do đó và đồng dạng (c.g.c). .	(1)
Ta lại có 	(2)
Từ (1) và (2) suy ra .
c) Áp dụng câu a. Đáp số: 
Bài 21 : Điểm là trung điểm cạnh đáy của tam giác cân . Các điểm và thứ tự thuộc các cạnh sao cho . Chứng minh rằng :
 	a)
b) Các tam giác và đồng dạng.
c) là tia phân giác của góc.
Hướng Dẫn :
a) và đồng dạng (g.g) 
Ta có BM = CM nên 
b) Từ và đồng dạng suy ra (Vì )
Ta lại có . Do đó và đồng dạng (c.g.c).
c) Từ câu b suy ra do đó DM là tia phân giác của góc BDE.