Giáo án dạy thêm Hình học Lớp 8 - Bài 3: Tính chất đường phân giác của một tam giác

BÀI 3: TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA MỘT TAM GIÁC
I. Tóm tắt lý thuyết
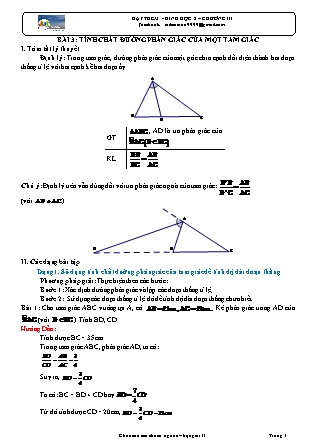
Định lý: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
GT
, AD là tia phân giác của 
KL
Chú ý: Định lý trên vẫn đúng đối với tia phân giác ngoài của tam giác: 
(với ).
II. Các dạng bài tập
Dạng 1. Sử dụng tính chất đường phân giác của tam giác để tính độ dài đoạn thẳng
Phương pháp giải: Thực hiện theo các bước:
Bước 1: Xác định đường phân giác và lập các đoạn thẳng tỉ lệ;
Bước 2: Sử dụng các đoạn thẳng tỉ lệ đó để tính độ dài đoạn thẳng chưa biết.
Bài 1: Cho tam giác ABC vuông tại A, có Kẻ phân giác trong AD của (với ). Tính BD, CD.
Hướng Dẫn:
	Tính được BC = 35cm. 
Trong tam giác ABC, phân giác AD, ta có: 
Suy ra, 
Ta có: BC = BD + CD hay .
Từ đó tính được CD = 20cm, 
Bài 2: Cho tam giác ABC vuông tại A. Kẻ phân giác trong AD của (với ), biết Tính độ dài các đoạn thẳng AB, AC.
Hướng Dẫn:
	Ta có: BC = BD + CD = 35cm.
Ta chỉ ra được 
Trong vuông cân tại A, ta có:
Từ đó tính được
Dạng 2. Sử dụng tính chất đường phân giác của tam giác để tính tỉ số, chứng minh các hệ thức, các đoạn thẳng bằng nhau, các đường thẳng song song
Phương pháp giải: Thực hiện theo các bước sau:
Bước 1: Xác định đường phân giác và lập các đoạn thẳng tỉ lệ;
Bước 2: Sử dụng các tỉ số đã có, cùng với tính chất của tỉ lệ thức, các tỉ số trung gian (nếu cần) và định lý đảo của định lý Ta – lét để tính tỉ số đoạn thẳng hoặc chứng minh các hệ thức, từ đó suy ra các đoạn thẳng bằng nhau hay các đường thẳng song song.
Bài 1: Cho hình thang ABCD (AB// CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh bên AD, BC theo thứ tự tại E và F.Chứng minh rằng : OE = OF
Hướng Dẫn:
	Sơ đồ giải 
OE = OF
Ý
 = 
Ý
 = ; = ; =
Ý Ý Ý
DAEC DBOF DAOB
DADC DBDC DCOD
 	Ý Ý
 EF // DC AB // CD
Ý
 gt
Bài 2: Cho tam giác ABC có các đường phân giác AD, BE, CF.
a) Chứng minh .
b) Khi tam giác ABC cân tại A, chứng minh EF song song với BC.
c) Biết , tính tỉ số diện tích của hai tam giác ABD và ACD.
Hướng Dẫn:
a) Cách 1. Sử dụng định lý Xe va đã chứng minh ở Câu 9 Bài 2.
Cách 2. Có thể chứng minh như sau: Xét tam giác ABC, phân giác AD, ta có: 
Tương tự, ta chứng minh được: 
Vậy .
b) Tam giác ABC cân tại A nên AB = AC
Suy ra, ta có: . Vậy theo định lý Ta-lét đảo, ta có ĐPCM.
c) Dễ thấy . Gọi h là chiều cao từ đỉnh A tới đáy BC, ta có:
Bài 3: Cho tam giác ABC, các đường phân giác AD, BE, CF giao nhau tại I. Chứng minh:
a) ;	b) 
Hướng Dẫn:
a) Trong tam giác ABD, phân giác BI, ta có: 
Tương tự, ta có: 
Theo tính chất dãy tỉ số bằng nhau, ta có: 
Suy ra, 
b) Sử dụng kết quả câu a)
Bài 4: Cho tam giác ABC (AB < AC), đường phân giác AD của (với ). Từ trung điểm M của BC, kẻ một đường thẳng song song với AD, cắt AC tại F và cắt tia đối của tia AB tại E. Chứng minh BE = CF.
Hướng Dẫn:
 (góc đồng vị)
 (góc so le trong)
Nên ta có cân tại A
Từ đó, ta có: EA = FA
Ta chứng minh được: BE = CF
Bài 5: Cho hình bình hành ABCD. Phân giác của và cắt các đường chéo BD và AC lần lượt tại M và N. Chứng minh: MN song song với AD.
Hướng Dẫn:
Gọi I là giao điểm của BD và AC.
Xét tam giác ABD, phân giác AM, ta có: 
Tương tự, ;
Mà AB =CD, suy ra 
Từ đó, ta có:
Suy ra ĐPCM.
III. Bài tập tự luyện
Bài tập cơ bản
Bài 1: Cho tam giác ABC, đường phân giác của góc BAC cắt cạnh BC tại D.
Tính tỉ số biết AB = 3cm; AC = 5cm
Tính độ dài DC, biết BD = 1,5cm
Hướng Dẫn:
a)AD là phân giác của , ta có
. Vậy 
b) 
hay 
Bài 2: Cho tam giác ABC cân ở A, phân giác trong BD, BC = 10cm, AB = 15cm.Tính AD, DC.
Hướng Dẫn:
BD là phân giác trong của góc B nên
Theo tính chất của tỉ lệ thức, ta có 
 (cm)
Ta có DA + DC = AC (cm)
Bài 3: Cho tam giác có . Vẽ đường phân giác AD.
a) Tính độ dài 
Tia phân giác của góc cắt ở . Tính tỉ số 
Hướng Dẫn:
a) Theo tính chất đường phân giác góc của ta có:
. 
Do đó: 
 (cm). 
Suy ra DB = 30 cm
b)Theo tính chất đường phân giác góc của 
Ta có: 	
Chú ý: Nếu có thì (bạn đọc tự chứng minh)
Bài 4: Tam giác cân có . Đường phân giác của góc cắt đường cao ở. Biết . Tính độ dài .
Hướng Dẫn:
 là đường phân giác của nên 
Do đó .
Bài 5: Tam giác có chu vi , là cạnh lớn nhất của tam giác. Đường phân giác của góc chia thành hai đoạn thẳng tỉ lệ với Tính độ dài các cạnh của tam giác 
Hướng Dẫn:
Ta có nên 
Do đó 
Từ đó .
Bài 6: Tam giác có, các đường phân giác. Tính độ dài.
Hướng Dẫn:
 là đường phân giác góc nên 
Ta có nên 
Do đó .
Bài 7: Qua trung điểm của đoạn thẳng , vẽ tia , trên tia đó lấy điểm. Các tia phân giác của các góc và thứ tự cắt ở 
a) Chứng minh rằng song song với 
b) Điểm ở vị trí nào thì là đường trung bình của tam giác?
Hướng Dẫn:
a) là đường phân giác của nên 
 là đường phân giác của nên
	(2)
Ta lại có 
Nên từ suy ra , vậy 
b) là đường trung bình của tam giác do (1)
Bài 8: Cho tam giác ABC có 3 phân giác trong AM, BN, CP cắt nhau tại I. Chứng minh 
a) 
b) 
Hướng Dẫn: 
a) Ta có AM là phân giác của góc A
Theo tính chất đường phân giác trong tam giác, ta có 
Tương tự đối với các đường phân giác BN, CP ta có 
Do đó 
Vậy 
b) Gọi a, b, c lần lượt là độ dài của các cạnh BC, CA, AB
Trong thì BI là phân giác ứng với cạnh AM nên
 (1)
Trong thì CI là phân giác ứng với cạnh AM nên
Mà CM = BC – BM = a – BM . Nên (2)
So sánh (1) và (2) ta có 
Chứng minh tương tự ta có 
Suy ra 
Vậy 
Bài 9: Cho tam giác ABC, phân giác trong AD. Phân giác giác cắt AC tại F, phân giác cắt AB tại E. Chứng minh rằng 
a) 
b) AF.BE.CD = AE.BD.CF
Hướng Dẫn:
a) Áp dụng tính chất đường phân giác ta có 
 (1)
 (2)
Nhân (1) với (2) vế theo vế ta được: 
Do AD là phân giác góc A nên
Vậy 
b) Nhân (1) với (2) vế theo vế ta được
Hay 
Vậy AF.BE.CD = AE.BD.CF
Bài 10: Cho tam giác ABC, phân giác trong BD, CE. Chứng minh rằng 
a)Nếu DE//BC thì tam giác ABC cân tại A.
b)Nếu tam giác ABC cân tại A thì DE//BC.
Hướng Dẫn:
a) Giả sử DE//BC thì ta có (1)
Mặt khác, BD là phân giác góc B nên ta có và CE là phân giác góc C 
nên ta có 
Suy ra 
Nên cân tại A
b) Giả sử cân tại A 
Ta có BD là phân giác góc B
nên ta có và CE là phân giác góc C nên ta có 
Mặt khác 
Suy ra DE//BC
Bài 11: Cho hình bình hành ABCD Trên tia đối của tia CD lấy điểm E sao cho . Đường thẳng BE cắt đường thẳng AD tại M. Đường thẳng CM cắt AB tại F, BD tại K. Chứng minh rằng
a) 
b) 
c) 
Hướng Dẫn:
a)Ta có BC//DM 
 	Ta lại có FB//DC 
Suy ra 
b)Ta có BC//DM 
 (1)
Ta lại có FB//DC
 (2)
Lấy (1) cộng (2) vế theo vế ta được : 
Vậy 
c) Ta có suy ra BC là phân giác góc B
Theo tính chất phân giác ta có (3)
Mặt khác, ta có FB//CE 
AF//DC 
Suy ra (4)
Từ (3) và (4) suy ra 
Bài 12: Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Đường thẳng vuông góc với BC tại D cắt AC tại E. Gọi M là trung điểm của BE, tia AM cắt BC tại G. Chứng minh: .
Hướng Dẫn:
Ta chứng minh: . Ta có: DE // AH .
Dựng đường thẳng qua E vuông góc AH tại I, suy ra HIED là hình chữ nhật.
IE = HD = HA; do đó hai tam giác vuông IEA và HBA bằng nhau.
.
Vì M là trung điểm BE, tam giác ABE cân tại A nên AM là tia phân giác góc hay G là chân đường phân giác trong góc trong tam giác ABC. Từ đó ta có:
. Vậy .
Bài 13: Cho tam giác ABC, các đường phân giác AD, BE, CF. Biết Tính độ dài các đoạn BD, DC, EA, EC, FA, FB.
Hướng Dẫn:
Bài 14: Cho tam giác ABC, Đường phân giác của và cắt cạnh AC và AB lần lượt tại D và E.
a) Tính độ dài các đoạn thẳng AE, EB, AD, DC.
b) Trên cạnh BC lấy điểm K sao cho Chứng minh ba đường thẳng AK, BD, CE đồng quy.
Hướng Dẫn:
a) Học sinh tự giải
b) Ta lập được tỉ số ; Từ đó ta có AK là phân giác góc . Nên suy ra ĐPCM.
Bài 15: Cho tam giác ABC, trung tuyến AM. Phân giác của cắt AB ở D, phân giác của góc cắt AC ở E.
a) Chứng minh DE song song với BC.
b) Gọi I là giao điểm của DE với AM. Chứng minh I là trung điểm của DE.
Hướng Dẫn:
a) Xét tam giác AMB, phân giác MD, có 
Tương tự ta chứng minh được 
Từ đó ta có 
Suy ra DE//BC.
b) Vì DE//BC nên 
Mà MB = MC, suy ra DI = IE
Bài 16: Cho tam giác ABC vuông tại A, đường phân giác BD.
a) Tính các độ dài DA, DC.
b) Tia phân giác của cắt BD ở I. Gọi M là trung điểm của BC. Chứng minh 
Hướng Dẫn:
a) Học sinh tự thực hiện.
b) Từ phần a, ta có: MB = MC = 5cm
Suy ra 
Nên .
Trong tam giác BIM, có , là góc ngoài nên ta có:
Tương tự, 
Vậy 
Bài 17: Cho tam giác ABC có . Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm tam giác ABC.
a) Chứng minh IG song song với BC.
b) Tính độ dài đoạn thẳng IG.
Hướng Dẫn:
Gọi M là trung điểm của BC.AD là tia phân giác góc BAC (D nằm trên BC)
Tính được CD = 9cm.
Trong tam giác ACD, phân giác CI, ta có: 
Ta chứng minh được 
Nên ta suy ra từ đó có được ĐPCM.
b) Ta tính được DM = 1,5cm.
Vì IG//DM, nên 
Bài 18: Cho tam giác ABC cân ở A, BC = 8cm, phân giác của góc B cắt đường cao AH ở K, .
	a) Tính độ dài AB.
	b) Đường thẳng vuông góc với BK cắt AH ở E. Tính EH.
Hướng Dẫn:
a) AB = 6cm	b) EH = 8,94 cm.
Bài 19: Cho tam giác ABC có độ dài các cạnh AB = m, AC = n; AD là đường phân giác trong của góc A. Tính tỉ số diện tích của tam giác ABD và tam giác ACD.
Hướng Dẫn:
.
Bài 20: Cho tam giác ABC cân ở A, phân giác trong BD, BC = 10cm, AB = 15cm.
	a) Tính AD, DC.
	b) Đường phân giác ngoài của góc B của tam giác ABC cắt đường thẳng AC tại D¢. Tính D¢C.
Hướng Dẫn:
a) DA = 9cm, DC = 6cm	b) D¢C = 10cm.
Bài 21: Cho tam giác ABC, trung tuyến AM và đường phân giác trong AD.
	a) Tính diện tích tam giác ADM, biết AB = m, AC = n (n > m) và diện tích DABC bằng S.
	b) Cho n = 7cm, m = 3cm. Diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC?
Hướng Dẫn:
a) 	b) .
Bài 22: Cho tam giác ABC có AB = 5cm, AC = 6cm, BC = 7cm. Gọi G là trọng tâm tam giác ABC, O là giao điểm của hai đường phân giác BD, AE.
	a) Tính độ dài đoạn thẳng AD.
	b) Chứng minh OG // AC.
Hướng Dẫn:
a) 	b) OG // DM Þ OG // AC.
Bài 23: Cho tam giác ABC, trung tuyến AM, đường phân giác của góc AMB cắt AB ở D, đường phân giác của góc AMC cắt cạnh AC ở E. Chứng minh DE // BC.
Hướng Dẫn:
.
Bài 24: Cho tam giác ABC (AB < AC), AD là phân giác trong của góc A. Qua trung điểm E của cạnh BC, vẽ đường thẳng song song với AD, cắt cạnh AC tại F, cắt đường thẳng AB tại G. Chứng minh CF = BG.
Hướng Dẫn:
.
Bài 25: Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N.
	a) Chứng minh rằng MM // BC.
	b) Tam giác ABC phải thoả điều kiện gì để có MN = AI?
	c) Tam giác ABC phải thoả điều kiện gì để có MN ^ AI?
Hướng Dẫn:
a) Chứng minh .
Bài 26: Cho hình thang cân ABCD, đáy lớn DC, góc D = 600 . Đường phân giác của góc D cắt đường chéo AC tại I, chia AC thành hai đoạn theo tỉ số và cắt đáy AB tại M. Tính các cạnh đáy AB, DC, biết MA – MB = 6cm.
Hướng Dẫn:
Chứng minh DC = AB + AD Þ DC = AB + AM Þ Þ DC = 66cm, AB = 42cm.
Bài 27: Cho hình bình hành ABCD. Một đường thẳng cắt AB ở E, AD ở F và cắt đường chéo AC ở G. Chứng minh hệ thức: .
Hướng Dẫn:
Vẽ DM // EF, BN // EF. Áp dụng định lí Ta-lét vào các tam giác ADM, ABN.
Bài 28: Cho hình bình hành ABCD. Trên cạnh AB lấy một điểm M và trên cạnh CD lấy một điểm N sao cho DN = BM. Chứng minh rằng ba đường thẳng MN, DB, AC đồng quy.
Hướng Dẫn:
Bài 29: a) Chứng minh rằng tia đi qua đỉnh của một góc của tam giác và chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy là tia phân giác của góc đó.
b) Cho tam giác có , các đường phân giác . Chứng minh rằng 
Hướng Dẫn:
Kẻ thì . Theo giả thiết ta có . Suy ra . Do đó 
Ta lại có nên , từ đó 
Chú ý: Bài toán trên là định lý đảo của tính chất đường phân giác của tam giác
b) 
Qua C vẽ đường thẳng song song với DA, cắt BA ở K. 
Dễ thấy ACK là tam giác đều. 
Ta có: , 
Do đó là tia phân giác của góc (theo kết quả của câu a)
Chứng minh tương tự, là tia phân giác của góc 
Vậy (vì DE, DF là các tia phân giác của hai góc kề bù)
Chú ý: Cách giải khác chỉ dùng kiến thức lớp 7:
 có là phân giác góc ngoài, là phân giác góc trong nên là phân giác góc ngoài. 
Vậy là phân giác của góc .
Tương tự là phân giác của góc . Do đó 
Bài tâp nâng cao
Bài 1 : Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC), N là trung điểm của AB. Biết AB=6cm, AC=8cm. 
a) Vẽ AK là tia phân giác của góc (K thuộc BC). Tính AK? 
b) Gọi E là hình chiếu vuông góc của H lên AC và T là điểm đối xứng của N qua I với I là giao điểm của CN và HE. Chứng minh tứ giác NETH là hình bình hành.
Hướng Dẫn:
a) Theo tính chất chân đường phân giác trong ta có: 
. 
Gọi K’ là hình chiếu vuông góc của K lên AC, suy ra KK’ // AB. Theo định lí Talet ta có:
.
Mặt khác, tam giác AKK’ vuông cân tại K’ nên:
.
b) Ta chứng minh I là trung điểm của HE.
Vì HEAC nên HE // BA. Theo định lí Talet ta có: . 
Vì NA = NB nên IE = IH. Do đó I là trung điểm của HE.
Theo giả thiết thì I là trung điểm của NT.
Tứ giác NETH có hai đường chéo NT và EH có chung trung điểm I nên NETH là hình bình hành.
Bài 2: Cho ABC, có < 600 phân giác AD
a) Chứng minh AD < AB
b) Gọi AM là phân giác của ADC. Chứng minh rằng BC > 4 DM
Hướng Dẫn:
a)Ta có > = 
> AD < AB
 b) Gọi BC = a, AC = b, AB = c, AD = d
Trong ADC, AM là phân giác ta có
DM = ; CD = ( Vận dụng bài 1) DM = 
Để c/m BC > 4 DM ta c/m a > hay (b + d)(b + c) > 4bd (1)
Thật vậy : do c > d (b + d)(b + c) > (b + d)2 4bd . Bất đẳng thức (1) được c/m
Bài 3:Cho ABC, trung tuyến AM, các tia phân giác của các góc AMB , AMC cắt AB, AC theo thứ tự ở D và E
a) Chứng minh DE // BC
b) Cho BC = a, AM = m. Tính độ dài DE
c) Tìm tập hợp các giao diểm I của AM và DE nếu ABC có BC cố định, AM = m không đổi
d) ABC có điều kiện gì thì DE là đường trung bình của nó
Hướng Dẫn:
a) MD là phân giác của nên (1)
 	ME là phân giác của nên (2)
Từ (1), (2) và giả thiết MB = MC ta suy ra DE // BC
b) DE // BC . Đặt DE = x 
c) Ta có: MI = DE = không đổi 
 I luôn cách M một đoạn không đổi nên tập hợp các điểm I là đường tròn tâm M, bán kính MI = (Trừ giao điểm của nó với BC)
d) DE là đường trung bình của ABC DA = DB MA = MB ABC vuông ở A
Bài 4: Cho ABC ( AB < AC) các phân giác BD, CE
a) Đường thẳng qua D và song song với BC cắt AB ở K, chứng minh E nằm giữa B và K
b) Chứng minh: CD > DE > BE
Hướng Dẫn:
a) BD là phân giác nên 
 (1)
Mặt khác KD // BC nên (2)
Từ (1) và (2) suy ra 
E nằm giữa K và B
b)Gọi M là giao điểm của DE và CB. 
Ta có (Góc so le trong) 
 	Mà E nằm giữa K và B nên >>> EB < DE
Ta lại có >> (Vì = )
Suy ra CD > ED CD > ED > BE
Bài 5: Cho ABC với ba đường phân giác AD, BE, CF. Chứng minh
a. .
b. . 
Hướng Dẫn:
a)AD là đường phân giác của nên ta có: (1)
Tương tự: với các phân giác BE, CF ta có: (2) ; (3)
Từ (1); (2); (3) suy ra: = 1
b) Đặt AB = c , AC = b , BC = a , AD = da. 
Qua C kẻ đường thẳng song song với AD , cắt tia BA ở H. 
Theo ĐL Talét ta có: 
Do CH < AC + AH = 2b nên: 
Chứng minh tương tự ta có : Và Nên: 
 ( đpcm )
Bài 6: Cho tam giác ABC và ba đường phân giác AM, BN, CP cắt nhau tại O. Ba cạnh AB, BC, CA tỉ lệ với 4, 7, 5.
	a) Tính MC, biết BC = 18cm.
	b) Tính AC, biết NC – NA = 3cm.
	c) Tính tỉ số .
	d) Chứng minh: .
	e) Chứng minh: .
Hướng Dẫn:
a) MC = 10cm	
b) AC = 11cm	
c) 	
	e) Vẽ BD // AM Þ BD < 2AB Þ Þ .
	Tương tự: , Þ đpcm.
Bài 7: Cho tam giác có , các đường phân giác .
a) Tính độ dài rồi suy ra 
b) Vẽ hình bình hành . Chứng minh rằng 
c) Chứng minh rằng .
Hướng Dẫn:
a) Tính độ dài các cạnh , ta được (xem ví dụ 6)
Ta lại có nên tức là .
b) Ta có mà nên , suy ra	(1)
Ta lại có nên , mà nên 
Từ (1) và (2) ta suy ra 
c) mà nên .
Chú ý: Từ bài toán trên suy ra:
- Trong tam giác có hai cạnh không bằng nhau, đường phân giác ứng với cạnh lớn hơn thì nhỏ hơn.
- Tam giác có hai đường phân giác bằng nhau là tam giác cân (Một cách chứng minh bài toán này, xem Các bài tập và chuyên đề về tam giác)
Bài 8: Chứng minh rằng tia phân giác góc ngoài đỉnh của tam giác chia ngoài cạnh theo tỉ số .
Hướng Dẫn:
Gọi E là giao điểm của tia phân giác góc ngoài đỉnh với đường thẳng . 
Vẽ thì 	(1)
 (2)
Từ (1) và (2) suy ra 
Bài 9: Cho tam giác ABC có BC = a, CA = b, AB = c. Phân giác trong của góc A cắt BC tại D, phân giác ngoài góc A cắt BC tại E. Tính BD, DC, EB,EC theo a, b, c.
Hướng Dẫn:
Theo tính chất đường phân giác trong tam giác ABC ta có
+ (tính chất dãy tỉ số bằng nhau)
+