Ma trận và đề kiểm tra học kì I môn Toán Lớp 8 (Có đáp án)

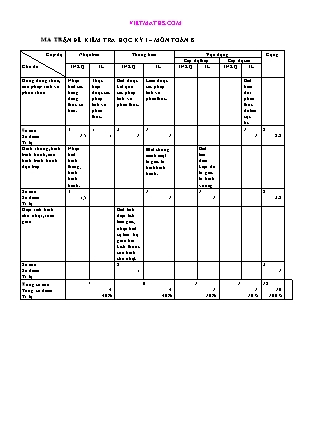
	MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I – MÔN TOÁN 8
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Hằng đẳng thức, các phép tính về phân thức
Nhận biết các hằng đẳng thức cơ bản.
Thực hiện được các phép tính về phân thức.
Biết được kết quả các phép tính về phân thức.
Làm được các phép tính về phân thức.
Biết biến đổi phân thức để tìm cực tri.
Số câu
Số điểm
Tỉ lệ
3
1,5
1
1
2
1
1
1
1
1
8
5,5
Hình thang, hình bình hành, các hình bình hành đặc biệt
Nhận biết hình thang, hình bình hành.
Biết chứng minh một tứ giác là hình bình hành. 
Biết tìm điều kiện để tứ giác là hình vuông
Số câu
Số điểm
Tỉ lệ
3
1,5
1
1
1
1
5
3,5
Diện tích hình chữ nhật, tam giác
Biết tính diện tích tam giác, nhận biết sự liên hệ giữa hai kích thước của hình chữ nhật.
Số câu
Số điểm
Tỉ lệ
2
1
2
1
Tổng số câu
Tổng số điểm
Tỉ lệ
7
4
40%
6
4
40%
1
1
10%
1
1
10%
15
10
100%
ÑAÙP AÙN – BIEÅU ÑIEÅM ÑEÀ KIEÅM TRA HOÏC KYØ 1 - 	MOÂN TOAÙN 8
I. TRAÉC NGHIEÄM (5 ñieåm)
Caâu 1 (2 ñieåm). Ñieàn daáu “X” thích hôïp, moãi keát quaû ñuùng ñöôïc 0,5 ñieåm
1. Sai 	2. Ñuùng 	3. Ñuùng 	4. Sai 
Caâu 2 (3 ñieåm). Khoanh troøn vaøo noät chöõ caùi in hoa ôû ñaàu caâu traû lôøi ñuùng nhaát, moãi keát quaû ñuùng ñöôïc 0,5 ñieåm
1. B	2. D	3. D	4. C	5. A	6. C
II. TÖÏ LUAÄN (5 ñieåm)
Baøi 1 (2 ñieåm). Thöïc hieän caùc pheùp tính:
a) Thöïc hieän pheùp chia vaø ruùt goïn ñuùng keát quaû: 	(1 ñieåm)
b) Thöïc hieän pheùp tính trong ngoaëc ñöôïc: 	(0,5 ñieåm)
Thay vaøo vaø tính ñuùng keát quaû: - x	(0,5 ñieåm)
Baøi 2 (2 ñieåm).
Veõ hình ñuùng ñöôïc 	(0,25 ñieåm)
	a) Söû duïng tính chaát ñöôøng trung bình cuûa tam giaùc ñeå suy ra:
MN // BC vaø MN = BC, QP // BC vaø QP = BC (0,5 ñieåm)
Chæ ra MN // QP vaø MN = QP vaø keát luaän töù giaùc 
MNPQ laø hình bình haønh.	(0,5 ñieåm)
b) Neâu ñöôïc ñeå hình bình haønh MNPQ trôû thaønh 
hình vuoâng thì MN = MQ vaø = 900 
(MN ^ MQ).	(0,5 ñieåm)
Söû duïng tính chaát ñöôøng trung bình cuûa tam giaùc 
ñeå suy ra AD = BC vaø AD ^ BC.	
Keát luaän: Ñeå töù giaùc MNPQ laø hình vuoâng thì töù giaùc 
ABCD phaûi coù AD = BC vaø AD ^ BC.	(0,25 ñieåm)
Baøi 3 (1 ñieåm).
A = = 
Tieáp tuïc bieán ñoåi ñeå bieåu thöùc A ñöôïc keát quaû A = 	(0,5 ñieåm)
Nhaän xeùt ñöôïc: A = ³ 
Suy ra daáu “=” xaûy ra khi vaø chæ khi x – 2011 = 0 Û x = 2011.
Keát luaän ñöôïc: Khi x = 2011 thì bieåu thöùc A ñaït giaù trò nhoû nhaát laø: 	(0,5 ñieåm)
*) Ghi chuù: Caùc caùch giaûi khaùc ñuùng, chính xaùc ñöôïc ghi ñieåm toái ña cho moãi caâu.
TRÖÔØNG THCS 
Hoï teân: 	
Lôùp:	
KIEÅM TRA HOÏC KYØ 1 –MOÂN TOAÙN 8 Thôøi gian: 90 phuùt
Ngaøy:	 thaùng	naêm	
Maõ phaùch
CHÖÕ KYÙ GIAÙM THÒ 1
CHÖÕ KYÙ GIAÙM THÒ 2
"
Ñieåm baèng soá
Ñieåm baèng chöõ
Chöõ kyù GK1
Chöõ kyù GK2
Maõ phaùch
ÑEÀ
I. TRAÉC NGHIEÄM (5 ñieåm) – Mỗi câu 0,5 điểm
Caâu 1 (2 ñieåm). Ñieàn daáu “X” thích hôïp vaøo oâ Ñuùng hoaëc Sai töông öùng vôùi moãi phaùt bieåu sau:
Noäi dung
Ñuùng
Sai
1. (x – y)3 = (y – x)3
2. Pheùp chia ña thöùc 6x3 – 17x2 + 11x – 2 cho ña thöùc 6x2 – 5x + 1 coù thöông laø x – 2.
3. Hình bình haønh coù hai ñöôøng cheùo vuoâng goùc vôùi nhau laø hình thoi.
4. Neáu chieàu daøi vaø chieàu roäng cuûa moät hình chöõ nhaät taêng leân 4 laàn thì dieän thì dieän tích hình chöõ nhaät taêng leân 8 laàn.
Caâu 2 (3 ñieåm). Mỗi câu 0,5 điểm. Khoanh troøn vaøo moät chöõ caùi in hoa ôû ñaàu caâu traû lôøi ñuùng nhaát:
1. Keát quaû cuûa pheùp nhaân 3x2y(2x3y2 – 5xy + 1) baèng:
A. 6x5y3 + 15x3y2 + 3x2y 	B. 6x5y3 – 15x3y2 + 3x2y 	C. 6x5y3 – 5xy + 1 	D. Keát quaû khaùc
2. Giaù trò cuûa bieåu thöùc x2 – 5x + xy – 5y taïi x = 2010; y = - 2011 baèng:
A. 2015 	B. – 2015	C. 2005	D. – 2005
3. Giaù trò x thoûa maõn x2 + 6x + 9 = 0 laø:
A. x = 6	B. x = - 6	C. x = 3	D. x = - 3
4. Ña thöùc M trong ñaúng thöùc laø:
A. 3x2 – 5	B. 3x2 + 5	C. 3x2 – 15x 	D. 3x2 + 15x
5. Cho hình thang ABCD (AB // CD) coù = 1000 thì:
A. = 800	B. = 1000	C. = 800	D. = 1000
6. Cho tam giaùc MNQ vuoâng taïi M, coù MN = 8cm, NQ = 10cm. Dieän tích cuûa tam giaùc vuoâng MNQ baèng:
A. 48cm2	B. 40cm2	C. 24cm2	D. 12cm2
II. TÖÏ LUAÄN (5 ñieåm)
Baøi 1 (2 ñieåm). Thöïc hieän caùc pheùp tính sau:
a) ; 	b) 
Baøi 2 (2 ñieåm). Cho töù giaùc ABCD. Goïi M, N, P, Q laàn löôït laø trung ñieåm cuûa AB, AC, CD, DB.
a) Töù giaùc MNPQ laø hình gì? Vì sao?
b) Tìm ñieàu kieän cuûa töù giaùc ABCD ñeå töù giaùc MNPQ laø hình vuoâng?
Baøi 3 (1 ñieåm). Cho bieåu thöùc A = vôùi x > 0.
Tìm giaù trò cuûa x ñeå bieåu thöùc A ñaït giaù trò nhoû nhaát. Tìm giaù trò nhoû nhaát ñoù.
Baøi laøm: